Как определить фокусное расстояние: Определение фокусного расстояния объектива
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
Стр 1 из 4Следующая ⇒ ЛАБОРАТОРНАЯ РАБОТА №3 Определение фокусного расстояния линзы Цель работы.Определение фокусного расстояния собирающей и рассеивающей линз. Приборы и принадлежности:направляющая, набор рейтеров, лазер, призма, набор линз, экран, линейка,штангенциркуль. Построение изображения в тонкой линзе. Под построением изображения понимают действие, в результате которого по известному положению (а) источника (предмета) и величине фокусного расстояния (f) находят положение изображения (b). Результат может быть достигнут путём расчёта или графического построения. Ограничимся только графическим построением.
Построение изображения точки S, расположенной на главной оптической оси собирающей линзы, на расстоянии большем f1,. Проводят произвольно побочную оптическую ось OQ до пересечения с задней фокальной плоскостью. Затем проводят линию SA, параллельно побочной оптической оси OQ. Линия AQ пересекает главную оптическую ось в точке S1, которая и есть изображение точки S. Полученное изображение является действительным. Построение изображение в рассеивающей линзе (рис.3.5). Т.к фокус для этой (рассеивающей) линзы является мнимым, то.проводят произвольно побочную оптическую ось QО до пересечения с передней фокальной плоскостью. Затем проводят луч SA, параллельный побочной оптической оси QО. Прямая QA определит направление преломлённого луча. Пересечение обратного продолжения преломлённого луча с главной оптической осью укажет точку S1, являющейся мнимым изображением точки S. Определение положения точки, в которой собирается сходящийся пучок лучей, направленный на собирающую линзу (рис. Параллельно верхнему из сходящихся лучей проведём побочную оптическую ось. Она пересечёт заднюю фокальную плоскость в точке Q1. Побочная оптическая ось, параллельная нижнему из сходящихся лучей, пересечёт фокальную плоскость в точке Q2. Верхний преломлённый луч пойдёт по направлению к точке Q1, нижний — в направлении к Q2. Они пересекутся в точке S1. Определение положения точки, в которой собирается сходящийся пучок лучей, направленный на рассеивающую линзу (рис.3.6 В). Параллельно верхнему из сходящихся лучей проведём побочную оптическую ось. Она пересечёт переднюю фокальную плоскость в точке Q1. Побочная оптическая ось, параллельная нижнему из сходящихся лучей, пересечёт переднюю фокальную плоскость в точке Q
преломлённый луч пойдёт так, чтобы его обратное продолжение проходило через точку Q1, нижний — через точку Q2.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Упражнение 1. Определение фокусного расстояния собирающей (положительной) линзы в параллельных лучах. Выполнение упражнения. 1.Лазер, делительную призму, линзу и экран с использованием рейтеров расположить на направляющей (см. рис.3.7). Внимание! Все наблюдения за лазерным лучом во время настройки оптической схемы и выполнения задания производить только по картинкам на экране. 2 .Включить лазер. Установить делительную призму в луч лазера так, чтобы её грань разделяла луч. В этом случае на экране возникнет два световых пятна, соответствующих двум лучам. Перемещая призму по высоте, убедитесь в приблизительно одинаковой яркости обеих лучей. . 3.Передвигая экран по пазу, добиться, чтобы лучи сходились в одной точке. Если лучи не сходятся, переставить линзу в другое гнездо. Измерить расстояние L1 между серединой линзы и экраном. Рассчитайте оптическую силу линзы.
4.Проделать то, что указано в пункте 3 для линз 2 и 3. Рассчитать погрешность ΔL в определении L1 по формуле =tNP , где N — число измерений, Р — требуемая надёжность. Результаты измерений записать в виде: Фокусное расстояниелинзы 1— f1= (<L1> ΔL)см) Фокусное расстояние линзы 2— f2=……….. Фокусное расстояние линзы 3— f3=…
Упражнение 2. Определение фокусного расстояния рассеивающей линзы Поскольку для рассевающей линзы параллельные лучи сходиться не будут (фокус мнимый), то для нахождения фокуса такой линзы надо использовать сходящийся пучок лучей (рис 3.6 В). Расчёт фокусного расстояния производится с использованием формулы (3.5). В качестве предметной точки, для искомой линзы, используется фокус вспомогательной линзы, в котором сходятся параллельные лучи от лазера, прошедшие делительную призму. Источник (предмет) в этом случае является мнимым. Выполнение упражнения2.1. Установить на направляющей собирающую линзу 1 с известным фокусным расстоянием (f1=…) и рассеивающую линзу так, как показано на рис.3.8. Линза 1 в этом случае выполняет роль вспомогательной линзы. Для того, чтобы изображение, создаваемое линзой 2, было действительным, предметная точка (фокус линзы 1), как это уже отмечено, должна располагаться за линзой 2. 2. Проделать то, что указано в п. 1 упражнения 1. 3. Изменяя положение экрана, установитьего так, чтобы лучи, прошедшие линзу 2,сощлись в точке S1.. 4.. Измерить расстояние L между линзами и расстояние b2 между линзой 2 и экраном . Найти расстояние а2 = f1−L. (f1 определено вупражнении 1) 5. По формуле (3.5) найти фокусное расстояние f2 линзы 2. В этой формуле а = а2, b= b2. Рассчитайте оптическую силу линзы.
6 . Таблица 3.2 6. Рассчитать погрешность Δf в определении f2.
для надёжности α=0,95 и числа измерений N=5
. Записать результат f2=< f> . Оптическая сила линзы Д=… Контрольные вопросы 1. Какой раздел оптики называют геометрической оптикой? 2. Что такое тонкая линза и какие величины её характеризуют? 3. Как производится построение изображения в линзах при прохождении параллельных и сходящихся лучей? 4. Как экспериментально определить фокусные расстояния собирающей и рассеивающей линз? 5. Предложите свой метод определения фокусного расстояния рассеивающей линзы.
ЛАБОРАТОРНАЯ РАБОТА № 6 Изучение интерференция света, прошедшего через бипризму Френеля.
Цель работы: ознакомиться с одним из методов наблюдения интерференции света. Приборы и принадлежности: полупроводниковый лазер, оптическая скамья с набором рейтеров, бипризма Френеля, короткофокусная линза, экран для наблюдения с магнитными шайбами для крепления бумаги, линейка, карандаш, штангенциркуль.
Порядок выполнения работы. 1.Измерить фокус линзы f. Для этого, установить на оптической скамье лазер, линзу и экран.(рис.6.4). Включить лазер. Перемещая экран, найти такое его положение, при котором сечение светового луча было бы минимальным. В этом случае расстояние между линзой и экраном является фокусным расстоянием линзы f. 2.Определить угол пересечения лучей, прошедших бипризму Френеля (угол ψ). Для измерения угла ψ нужно установить рядом с лазером бипризму и на максимальном удалении от неё экран (рис.6.5). Включить лазер и проследить, чтобы его луч попадал на ребро бипризмы .
3. Измерить штангенциркулем расстояние 11 между световыми пятнами, которые наблюдаются на экране, удалённом на максимальное расстояние от призмы. Затем приблизить экран к призме на расстояние ∆L. Расстояние между световыми пятнами в этом случае сократится до l2. ψ= , (6.5) Измерение повторить пять раз. Ре-зультаты занести в таблицу 6.1 4.Установить линзу так, как показано на рис 6.6, повернув ее патрубком к призме. Экран установить на возможно большем удалении от линзы и закрепить на нём лист миллиметровой бумаги. Наблюдать на экране интерференционные полосы.
5. Принимая во внимание формулы (6.4 и 6.5), вычислить λi =
6. Изменяя положение экрана, повторить пункты 4 и 5 пять раз. Результаты записать в таблицу 6.2. 7.Погрешность полученных результатов рассчитать по формуле Δ 8. Результат измерения записать в виде l=(<λ>±Δl)мм
Контрольные вопросы 1. В чём сущность явления интерференции волн? 2. В чём особенность получения когерентных источников в оптике? 3. .Назвать условия возникновения максимумов и минимумов освещённости при интерференции. 4. Изобразить ход лучей в бипризме. 5. Вывести расчетную формулу для длины световой волны. 6. Указать порядок выполнения работы. 7. Предложите свой способ определения длины волы.
ЛАБОРАТОРНАЯ РАБОТА № 8. На дифракционной решётке. Цель работы:Изучение дифракционного спектра, возникающего при дифракции лазерного луча на дифракционной решётке. Определение с помощью дифракционной решётки длины световой волны, разрешающей способности и дисперсии различных дифракционных решеток. Приборы и принадлежности: лазер, набор дифракционных решеток, измерительная линейка, экран. Задание: С помощью дифракционной решётки определить длину световой волны,рассчитать дисперсию и разрешающую способность дифракционных решёток 1. Установить на направляющей необходимые части установки (рис.8.7). 2. С помощью магнитов прикрепить к экрану лист миллиметровой бумаги 3. Дифракционную решетку с известным периодом d — (d=1мм/число щелей приходящихся1 мм) 4. 5. Направить луч лазера на дифракционную решетку и, передвигая вдоль скамьи экран, установить его в таком положении, чтобы дифракционная картина занимала бы большую часть экрана, и при этом было бы видно наибольшее количество максимумов. 6. Перерисовать дифракционную картину на миллиметровую бумагу (Центры максимумов обозначить точкой). Отметить центральный максимум. 7. Выключить лазер. Снять бумагу и с возможной максимальной точностью штангенциркулем определить расстояние между центрами симметричных дифракционных максимумов. Результаты измерения занести в таблицу 8.1. 8. Измерить расстояние L от решетки до экрана. Снять миллиметровую бумагу. Измерить расстояния хm (х1, х2,и т.д.) между симметричными максимумами. Все результаты здесь и далее заносить в таблицу с обязательным указанием единиц измерения! 9. Вычислить значения тангенсов углов дифракции. По известным значениям рассчитать значения углов в радианах, а затем и синусов углов, соответствующих измеренным значениям хm.
12. По формулам (8.9) и (8.11) рассчитать угловую дисперсию D и разрешающую способность R дифракционной решетки. 13. Установить вторую и третью дифракционные решётки с другим числом щелей и проделать всё, что указано в пп.3—11. Обратить внимание на характер изменения дифракционной картин.
Определить для одной из решёток погрешность в определении длины волны , где tnα— коэффициент Стьюдента для числа измерений n = и надёжности α= 0.
Контрольные вопросы 1 Явление дифракции. 2. Принципы Гюйгенса-Френеля. 1. Дифракция Фраунгофера. 2. Условия максимумов и минимумов при дифракции на дифракционной решетке. 3. Объяснение дифракционной картины с помощью векторной диаграммы. 4. Получить условия для получения главных максимумов, для побочных минимумов и побочных максимумов. 5. Вывести формулу для интенсивности побочных максимумов 6.Угловая дисперсия дифракционной решетки. Разрешающая способность дифракционной решетки. 22. 23. . (11.1) 24. 25. Это равенство называется уравнением Эйнштейна для внешнего фотоэффекта. Из этого уравнения следует, что минимальная порция энергии, необходимая для вырывания электрона, должна быть равна работе выхода А. Следовательно, частота n0, соответствующая красной границе фотоэффекта, 26. 27. 28. На основании фотоэффекта действуют приёмники излучения, преобразующие световой сигнал в электрический. Такие устройства называются фотоэлементами. 29. Вакуумный фотоэлемент представляет собой откачанный стеклянный баллон, часть внутренней поверхности которого покрыта тонким слоем светочувствительного металла, выполняющего роль фотокатода. Анод А находится в центре баллона (рис.11.1). При освещении фотоэлемента из катода вылетают электроны и под действием электрического поля попадают на анод. По цепи идет ток.
31. 32. 33. Вольт-амперные и люкс-амперные характеристики фотоэлементов. 34. 35. Вольт — амперной характеристикой фотоэлемента называется кривая, выражающая зависимость фототока от напряжения. 36. 1. Вылетевшие с катода электроны образуют электронное облако. Под действием внешнего электрического поля часть электронов из электронного облака переходят на анод, создавая фототок. Чем больше электрическое поле, тем больше сила фототока. Фототок возрастает и при увеличении светового потока ( увеличения числа фотонов, попадающих в единицу времени на поверхность катода.). Фототок при увеличении напряжения будет возрастать, пока не возникнет динамическое равновесии между числом электронов, вылетевших из поверхности катода, и числом электронов, перешедших на анод. Соответствующая динамическому равновесию сила фототока и определяет величину силы тока насыщения. 37. 2 При изменении полярности приложенного напряжения внешнее поле будет не ускорять электроны, а задерживать их. Напряжение, при котором фототок окажется равным нулю, называется задерживающим напряжением (задерживающая разность потенциалов). 38. 39. , (11.3) 40. 41. где е, m и V — это заряд, масса и скорость электрона соответственно. 42. Люкс-амперной (или световой) характеристикой фотоэлемента называется зависимость фототока от освещенности катода (Е) при постоянном напряжении. У вакуумных фотоэлементов световая характеристика линейна, так как число выбитых электронов в единицу времени nпропорционально освещенности (Iн = е n ~ E). 43. Выполнение работы 45. 46. 1. Ознакомиться с имеющимися на лабораторном столе приборами. 47. 2.Снять вольт – ампер нуюхарактеристику вакуумного фотоэлемента (СЦВ-4):
48. 2.1. Поместив фотоэлемент СЦВ-4 на оптическую скамью, собрать электрическую цепь по рис.11.4. 49. 2.2. Подать напряжение сети на выпрямитель и источник света. Изменяя напряжение U, подаваемое на фотоэле Таблица11.1 50. мент, от 0 до (120-150)В, снять зависимость (7-10 точек) силы фототока Iфот напряжения для двух расстояний r1и r2 фотоэлемента от источника света. Результаты измерений занести в табл. 11.1. 51. 52. П р и м е ч а н и е. Расстояния r1 и r2 необходимо подбирать такими, чтобы шкала миллиамперметра использовалась как можно полнее. Фототок можно измерять в относительных единицах (в делениях шкалы прибора). 53. 2.3. По измеренным данным построить графики Iф = f (U). 54. 55. 3.1. При постоянном напряжении (U = cоnst) снять зависимость силы фототока Iфот освещенности Е фотоэлемента. Так как освещенность обратно пропорциональна квадрату расстояния r , то изменять ее можно путем изменения r. Результаты измерений занести в табл. 11.2. 56. 57. 58.
ЛАБОРАТОРНАЯ РАБОТА №3 Определение фокусного расстояния линзы Цель работы.Определение фокусного расстояния собирающей и рассеивающей линз. Приборы и принадлежности:направляющая, набор рейтеров, лазер, призма, набор линз, экран, линейка,штангенциркуль. 1234Следующая ⇒ Читайте также: Алгоритмические операторы Matlab Конструирование и порядок расчёта дорожной одежды Исследования учёных: почему помогают молитвы? Почему терпят неудачу многие предприниматели? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 746; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении… Основы обеспечения единства измерений: Обеспечение единства измерений — деятельность метрологических служб, направленная на достижение… Интересное: Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего. Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
Стр 1 из 2Следующая ⇒ В г.
Факультет: № 4 Кафедра: № 12
Лабораторная работа Определение фокусного расстояния линзы
Г. Северодвинск Лабораторная работа ФПО-2А5 Определение фокусного расстояния линзы 1. Цель и метод работы Изучение законов геометрической оптики; измерение фокусного расстояния собирающей линзы двумя способами и сопоставление полученных результатов. Определения фокусного расстояния рассеивающей линзы. Вывод рабочей формулы Рассмотрим метод построения изображения в линзе. Ход лучей 1–1′, 2–2′, 3–3′ показан на Рис. 3.
Все эти лучи пересекаются в точке S′, которая является изображением источника света S. Расстояния от предмета до линзы и от линзы до изображения (Рис.
Выразим из этого уравнения F, получим:
Уравнение (4) позволяет определить фокусное расстояние линзы, измерив значения d и f. Если расстояние между предметом и изображением больше учетверенного расстояния от линзы до изображения, то, перемещая линзу вдоль ее главной оптической оси, на экране можно получить увеличенное или уменьшенное изображение предмета. При этом источник света и экран остаются неподвижными. Рис. 4 показывает ход лучей от источника до экрана при получении увеличенного и уменьшенного изображения предмета. Обозначим d1 — расстояние от предмета и f1 — расстояние от экрана до линзы в первом положении; d2 — расстояние от предмета и f2 — расстояние от экрана до линзы во втором положении.
Здесь: f1 = L – d1, d2 = d1 + l и f2 = L – d2. Выразим из (5) и (6) равенств F:
— для первого положения и
— для второго положения. Т. к. левые части равны, то равны и правые. Приравняем их и подставим вместо d2, f2 и f1 их выражения через d1, получим: . Сократим на L, раскроем скобки и приведём подобные: 2d1l = Ll – l2. Выразим d1: , и подставим в (5): Преобразуя это равенство и выражая F , получим:
Таким образом, можно определить фокусное расстояние линзы, измерив перемещение линзы l и расстояние между предметом и экраном L. Описание экспериментальной установки Экспериментальная установка (Рис. 5) состоит из осветителя 1, модели предмета в виде жёлтой стрелки, нанесенной на поверхность матового стекла 2, собирающей линзы 3 и экрана 4. Все элементы крепятся в рейтерах, которые можно перемещать по оптической скамье 5. Осветитель через блок питания подключен к сети переменного тока напряжением 220В.
Осветитель направляет световые лучи на матовое стекло, которое рассеивает их по всем направлениям. Таким образом, нарисованная на поверхности матового стекла жёлтая стрелка, становится источником, лучи которого преломляются собирающей линзой и попадают на экран. Порядок выполнения работы Определения фокусного расстояния собирающей линзы Первый способ определения фокусного расстояния собирающей линзы 1. Расположить модуль, в котором находится матовое стекло вплотную к осветителю. 2. Установить экран на расстоянии 450 — 500 мм от модуля с матовым стеклом. 3. Перемещая подвижный рейтер с линзой, получить на экране четкое увеличенное изображение предмета (жёлтой стрелки). 4. С помощью линейки или по шкале оптической скамьи измерить расстояния от предмета до линзы d и от линзы до экрана f. 5. Сместив линзу на оптической скамье, снова получить четкое изображение предмета на экране и повторить измерения пункта 4. Получить пять опытных значений расстояний, которые внести в таблицу 1. Второй способ определения расстояния собирающей линзы 1. Установить экран на расстоянии 400 – 450 мм от модуля с матовым стеклом. 2. Линейкой или по шкале оптической скамьи измерить расстояние L между предметом и экраном. Погрешность измерения не должна превышать 1 мм. 3. Перемещая подвижный рейтер с линзой, получить на экране четкое увеличенное изображение предмета (жёлтой стрелки). 4. Определить положение линзы на оптической скамье (Х1). 5. Перемещая подвижный рейтер с линзой, получить на экране четкое уменьшенное изображение предмета (жёлтой стрелки). 6. Определить положение линзы на оптической скамье X2. 7. Повторить измерения пункта 3–6. Получить пять опытных значений величины Х1 и Х2, которые внести в таблицу 2. Определения фокусного расстояния рассеивающей линзы 1. Установить экран на расстоянии 700 мм от модуля с матовым стеклом. 2. Линейкой или по шкале оптической скамьи измерить расстояние L между предметом и экраном. Погрешность измерения не должна превышать 1 мм. 3. Поместить осветитель, рассеивающую и собирающую линзы, экран. Оптические оси линз должны совпадать! 4. Перемещая подвижные рейтеры с линзами, получить на экране четкое увеличенное изображение предмета (жёлтой стрелки). 5. Определить положение собирающей линзы на оптической скамье Х1 и рассеивающей линзы Y1. 6. Перемещая подвижные рейтеры с линзами, получить на экране четкое уменьшенное изображение предмета (жёлтой стрелки). 7. Определить положение собирающей линзы на оптической скамье Х2 и рассеивающей линзы Y2. 8. Повторить измерения пункта 4–7. Получить три опытных значений величины Х1, Х2 и Y1, Y2, которые внести в таблицу 3. Таблица 1 Измерение фокусного расстояния собирающей линзы (первый способ)
Таблица 2 Измерение фокусного расстояния собирающей линзы (второй способ)
Таблица 3 Измерение фокусного расстояния рассеивающей линзы
Контрольные вопросы 1. 2. Дать определение гомоцентрическому пучку. 3. Что такое линза? 4. Что называется фокусным расстоянием линзы? 5. Дать определение тонкой линзе. ЛИТЕРАТУРА 1. Трофимова Т.И. Курс физики. — М.: Высшая школа, 1990. 2. Зисман Г. Д., Тодес О. М. Курс общей физики.- М.: Наука, 1972. . Т.1 3. Яворский Е. М., Детлаф А. А. Справочник по физике. – М.: Наука, 1980. В г. Северодвинске
Факультет: № 4 Кафедра: № 12
Лабораторная работа Определение фокусного расстояния линзы
Г. Северодвинск Лабораторная работа ФПО-2А5 12Следующая ⇒ Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой. Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… |
3. Определение фокусного расстояния рассеивающей линзы
Определение фокусного расстояния рассеивающей линзы затрудняется тем, что изображение предмета получается мнимым и поэтому расстояния, входящие в формулу линзы не могут быть непосредственно измеряны.. Эту трудность легко обойти с помощью вспомогательной собирающей линзы. В начале опыта на оптическую скамью помещают только одну собирающую линзу и получают на экране действительное изображение предмета А (см рис.6). По линейке расположенной у основания оптической скамьи, отмечают положение D этого изображения
рис. 6.
6.
Если на пути лучей, выходящих из точки А и сходящихся в точке D после преломления их в собирающей линзе B (рис. 6), поставить рассеивающую линзу С так, чтобы расстояние CD было меньше её фокусного расстояния, то изображение точки А удалится от линзы В. Пусть оно переместится в точку Е (рис. 7).
.
рис. 7.
На рис. 7 показан ход лучей через рассеивающую линзу С. Совместим рисунки 6 и 7
. рис. 8.
или схематично это будет выглядеть так как показано на рис. 9.
рис. 9.
В силу оптического
принципа взаимности ( обратимость
световых лучей) можно мысленно рассмотреть
лучи, распространяющиеся из точки
E в обратную сторону.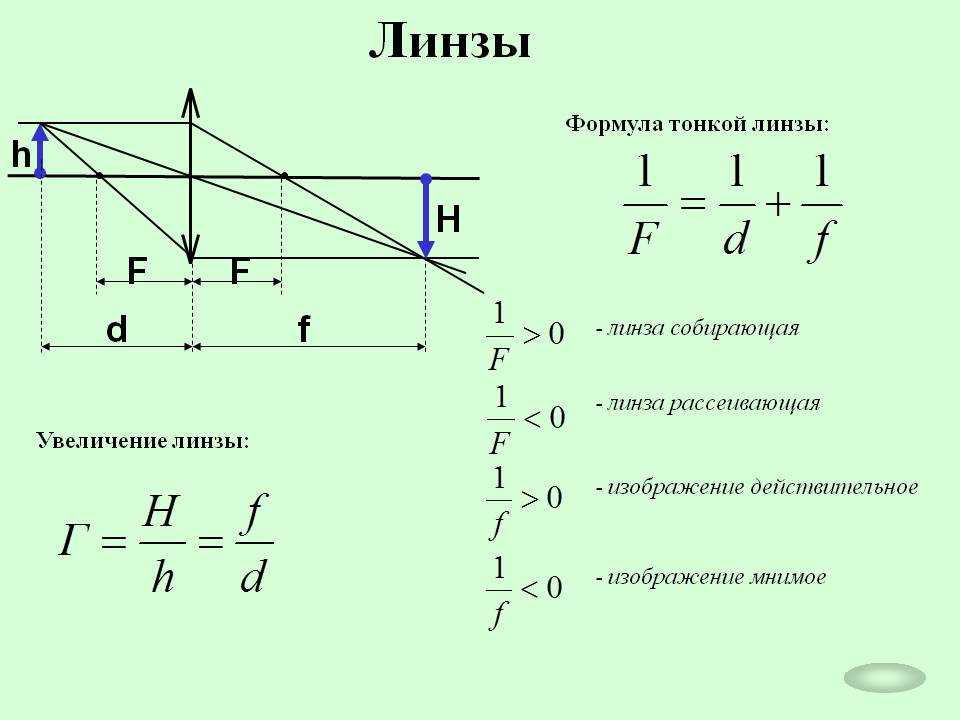 Тогда точка D будет
мнимым изображением точки E, расстояние
EC — расстоянием от линзы до объекта d, а
ДС — расстоянием от линзы до изображения
f. Учитывая правило знаков отметим, что
f- отрицательно, тогда можно записать
Тогда точка D будет
мнимым изображением точки E, расстояние
EC — расстоянием от линзы до объекта d, а
ДС — расстоянием от линзы до изображения
f. Учитывая правило знаков отметим, что
f- отрицательно, тогда можно записать
. (8)
Или . (9)
В работе используется оптическая скамья, на которой имеется шкала, позволяющая отмечать положение линз, экрана и объекта, перемещаемых по скамье, показанной на рис. 10.
рис.10.
На рис. 10: В — источник
света, Л — собирающая линза, Э — экран.
Установку на оптической скамье экрана,
линз и объекта (нити лампы) необходимо
производить так, чтобы их центры лежали
на одной прямой параллельной оптической
скамье, оптическая ось линзы должна
совпадать с этой прямой, а плоскость
экрана должна быть перпендикулярна
ей.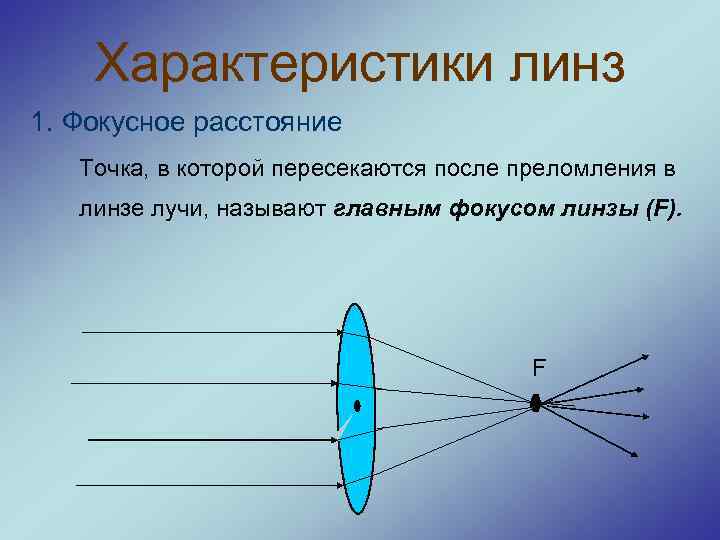
1 ОПРЕДЕЛЕНИЕ ГЛАВНОГО ФОКУСНОГО РАССТОЯНИЯ СОБИРАЮЩЕЙ ЛИНЗЫ ПО ПОЛОЖЕНИЮ ОБЪЕКТА И ЕГО ИЗОБРАЖЕНИЯ
1. Поместив экран на достаточно большом расстоянии от объекта ставят между ними линзу и передвигают её до тех пор, пока не получат на экране отчетливое увеличенное изображение объекта.
2. По шкале на оптической скамье отсчитывают расстояние d от объекта до линзы и расстояние f от линзы до изображения.
3. Полученные данные заносятся в таблицу 1.
4. Ввиду неточности визуальной оценки резкости изображения измерения (п.1-3) рекомендуется повторить не менее трех раз при разных положениях экрана.
5. Поместив экран на достаточно большом расстоянии от объекта, ставят между ними линзу и передвигают ее до тех пор, пока не получат на экране отчетливое уменьшенное изображение.
6. Повторяют пункты 2-4.
7. Из каждого отдельного
измерения по формуле (3) определяют
фокусное расстояние и из полученных
результатов находят среднее арифметическое.
8. Определяют оптическую силу линзы D.
5. Рассчитывают погрешность измерения.
Таблица 1
Номер опыта | d (м) | f (м) | F (м) | D=1/F (дп) | Примечание |
1 2 3 … 1 2 3 … | Увеличенное изображение Уменьшенное изображение |
II. ОПРЕДЕЛЕНИЕ ГЛАВНОГО ФОКУСНОГО РАССТОЯНИЯ СОБИРАЮЩЕЙ ЛИНЗЫ ПО ВЕЛИЧИНЕ ПЕРЕМЕЩЕНИЯ ЛИНЗЫ
. 1. Передвигая линзу по оптической скамье
при неизменном положении экрана и
источника света, получают на экране
резкое уменьшенное изображение нити
лампы. Записывают в таблицу 2 деление
шкалы х1, указывающее положения линзы
на скамье. Настройку и измерения
производят не менее трех раз.
1. Передвигая линзу по оптической скамье
при неизменном положении экрана и
источника света, получают на экране
резкое уменьшенное изображение нити
лампы. Записывают в таблицу 2 деление
шкалы х1, указывающее положения линзы
на скамье. Настройку и измерения
производят не менее трех раз.
2. Не изменяя расстояния между осветителем и экраном передвигают линзу на скамье так, чтобы получить на экране увеличенное изображение нити лампы. Записывают деление шкалы х2, соответствующее новому положению линзы. Измерения также повторяют не менее трех раз.
3. Определяют расстояние L между экраном и объектом по шкале оптической скамьи.
4. По данным таблицы 2 находят среднее значение величины перемещения линзы и рассчитывают фокусное расстояние линзы по формуле (7).
5. Рассчитывают погрешность измерения.
Таблица 2
Номер опыта. | l = x2-x1 (м) | L (м) | F (м) | ||
При уменьшенном изображении ( х1) | При увеличенном изображении ( х2) | ||||
1 2 3 и т.д. | |||||
Среднее значение х1 | Среднее значение х2 | ||||
Ш. ОПРЕДЕЛЕНИЕ ГЛАВНОГО ФОКУСНОГО РАССТОЯНИЯ РАССЕИВАЮЩЕЙ ЛИНЗЫ
1. Помещают между
экраном и объектом собирающую линзу.
Перемещая экран, добиваются резкого
изображения объект и записывают в
таблицу 3 деление шкалы, соответствующее
данному положению экрана ХD.
Помещают между
экраном и объектом собирающую линзу.
Перемещая экран, добиваются резкого
изображения объект и записывают в
таблицу 3 деление шкалы, соответствующее
данному положению экрана ХD.
2. Экран отодвигают от линзы, между собирающей линзой и первым положением экрана устанавливают рассеивающую линзу (рис .7)
3. Перемещая экран, получают на нем резкое изображение объекта. В таблицу 3 записывают деление шкалы ХE, соответствующее новому положению экрана.
4. Записывают деление шкалы ХC, где на скамье установлена рассеивающая линза.
5. Пункты 1-3 повторяют не менее трех раз. Для каждого из опытов находят значения величин d = ХC — ХE и f = ХC — ХD по формуле (8) подсчитывают фокусное расстояние F, а затем находят его среднее значение.
6. Рассчитывают погрешность измерения.
Таблица 3
Номер опыта | XC (м) | ХD (М) | ХЕ (м) | d = XC-XE (м) | f = ХС-ХD (м) | F (м) |
1 2 3 и т. | ||||||
Fср. |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется фокусом линзы ?
2. Что такое фокусное расстояние ?
3. Как располагается фокальная плоскость ?
4. Что называется оптической силой линзы ? В каких единицах она измеряется?
5. Как построить изображение в собирающей линзе ?
7. В чем заключается метод определения фокусного расстояния по величине перемещения линзы ?
8. Почему нельзя использовать методы определения фокусного расстояния
собирающих линз для рассеивающих линз?
9. Почему фокусное расстояние собирающей линзы должно быть меньше, чем у рассеивающей, если мы хотим с помощью собирающей линзы определить фокусное расстояние рассеивающей линзы?
10. Как рассчитываются погрешности
измерения фокусных расстояний линз ?
Как рассчитываются погрешности
измерения фокусных расстояний линз ?
Моделирование телеобъектива | УЧЕБНАЯ ТЕХНИКА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Лабораторная работа
Целью данной работы является изучение закономерностей преобразования гомоцентрических оптических лучей тонкими линзами и центрированной оптической системой.
Лабораторная работа разбита на четыре задания:
в первом производится центрировка элементов оптической системы;
второе и третье посвящены определению фокусных расстояний тонких линз различными методами;
в четвертом собирается сложная оптическая система и для нее измеряется фокусное расстояние.
Для формирования ясного понимания предлагаемой темы приводятся контрольные вопросы.
В работе используются: оптическая скамья с набором рейтеров. положительные и отрицательные линзы, экран, осветитель с ирисовой диафрагмой,
зрительная труба, светофильтры. кольцевые диа В большинстве реальных оптических систем содержится несколько преломляющих сферических поверхностей.
Оптическую систему называют центрированной. если центры всех поверхностей лежат на одной прямой, которую называют главной оптической осью системы.
В предлагаемой работе изучаются методы определения фокусных расстояний тонких собирающих и рассеиваю щих линз; определяются характеристики сложной системы, составленной из тонких линз. Световые пучки называются гомоцентрическим, если, выйдя из одной точки и пройдя оптическую систему, пучки или их продолжения снова сходятся в одной точке.
Определение фокусных расстояний положительных и отрицательных линз и положений главных плоскостей сложной оптической системы
Идеальной оптической системой называют систему, в которой сохраняется гомоцентричность пучков и изображение геометрически подобно предмету.
Как показывает теория, изображение предметов с помощью идеальной оптической системы может быть построено без детального исследования хода лучей внутри системы и требует только знания фо-
кусного расстояния и положения особых, так называемых главных плоскостей. Идеальная оптическая система, обладает осью симметрии, которая называется главной оптической осью.
Идеальная оптическая система, обладает осью симметрии, которая называется главной оптической осью.
Пусть ММ1 и NN1 — крайние поверхности, ограничивающие оптическую систему, а О1О2 — главная оптическая ось (рис. 1). Проведём луч А1 В1 , параллельный главной оптической оси. Этому лучу соответствует луч С 2D2 , выходящий из системы. Ход луча внутри оптической системы нас интересовать не будет. Точка F2 пересеизображением бесконечно удалённой точки. Точку F2
называют задним фокусом системы. Плоскость, перпендикулярная О1О2 и проходящая через точку F2, называется задней фокальной плоскостью. Задний фокус системы не всегда, конечно, лежит справа от нее,
как показано на рисунке 1. В рассеивающих системах задний фокус может лежать слева от всех оптических поверхностей, входящих в состав системы.
Рассмотрим теперь луч А2В2, входящий в систему справа и лежащий на продолжении луча А1В1. Слева из системы выйдет луч C1D1, сопряжённый лучу A2B2. Точку F1 называют передним фокусом системы. Исходящие из него лучи в пространстве изображений параллельны оптической оси. Продолжим теперь С1D1 и C2D2 до пересечения спродолжениями A1B1 и А2В2 и отметим точки пересечения
Исходящие из него лучи в пространстве изображений параллельны оптической оси. Продолжим теперь С1D1 и C2D2 до пересечения спродолжениями A1B1 и А2В2 и отметим точки пересечения
R1 и R2. Легко видеть, что эти точки сопряжены, т.е. являются изображением друг друга. Действительно, точка R1лежит на пересечении лучей A1B1 и С1D1, а точка R2 — напересечении сопряженных им лучей A2B2 и C2D2 (длябольшей наглядности направление одной нары сопряжён ных лучей, например, A2B2 и С1D1, можно изменить напротивоположное, пользуясь обратимостью световых лучей). Из построения ясно, что точки R1 и R2 лежат на одинаковом расстоянии от главной оптической оси, т.е. R1h2 = R2h3 (поперечное увеличение равно +1). Можно показать, что в идеальной системе все точки плоскости P1, перпендикулярной главной оптической оси и проходящей через R1, попарно сопряжены точкамплоскости P2, также перпендикулярной главной оптической оси и проходящей через R2- При этом сопряжённые
точки находятся на одинаковых расстояниях от оси (например, точки Q1 Q2). Плоскости P1и P2 называются главными плоскостями, а точки h2 и h3 – главными точкамисистемы. Расстояния от главных точек до фокусов называются фокусными расстояниями: f1=h2F1, f2=h3F2, в том случае, когда с обеих сторон системы находится одна и та же среда (например, воздух), f1 = f2 = f.
Плоскости P1и P2 называются главными плоскостями, а точки h2 и h3 – главными точкамисистемы. Расстояния от главных точек до фокусов называются фокусными расстояниями: f1=h2F1, f2=h3F2, в том случае, когда с обеих сторон системы находится одна и та же среда (например, воздух), f1 = f2 = f.
Если известно положение фокусов и главных плоскостей, изображение предмета может быть найдено путем простых геометрических построений. Рисунок 2 иллюстрирует эти построения. Удобно рассматривать лучи: а) падающие на линзу параллельно главной оптической оси; б) проходящие через передний фокус линзы; в) проходящие через центр линзы. Между главными плоскостями Р1 и Р2 все лучи следует
строить параллельно главной оптической оси. Для построения изображения точки необходимо рассмотреть ход двух любых лучей. Третий луч используют для проверки правильности построения изображения.
Оптическая система называется положительной или собирающей, если лучи, падающие на неё параллельно главной оптической оси, пройдя систему, отклоняются в направлении оси — собираются. Передний фокус F1 в этом случае лежит слева от главной плоскости P1, а задний фокус F2 — справа от P2. Если тe же лучи, пройдя систему, отклоняются от оси, — система называется отрицательной, или рассеивающей. При этом с оптической осью пересекаются не сами лучи, а их продолжения; F1 располагается правее P1, а F2 — левее P2. Фокусному расстоянию приписывается определённый знак: плюс для положительной системы и минус для отрицательной. Если ввести расстояния от предмета итизображения до соответствующих главных плоскостей, то легко установить соотношение между этими расстояниями и фокусным расстоянием системы:
Передний фокус F1 в этом случае лежит слева от главной плоскости P1, а задний фокус F2 — справа от P2. Если тe же лучи, пройдя систему, отклоняются от оси, — система называется отрицательной, или рассеивающей. При этом с оптической осью пересекаются не сами лучи, а их продолжения; F1 располагается правее P1, а F2 — левее P2. Фокусному расстоянию приписывается определённый знак: плюс для положительной системы и минус для отрицательной. Если ввести расстояния от предмета итизображения до соответствующих главных плоскостей, то легко установить соотношение между этими расстояниями и фокусным расстоянием системы:
а а f1 1 1
1 2
+ =
В формуле (1) а1 считается положительным, если Рис. 5. Измерение фокусного расстояния
оптической системы по методу Аббе
Фокусное расстояние толстой положительной линзы
определяют по методу Аббе (рис. 5). Пусть предмет, ли-
нейный размер которого равен у, находится на расстоя-
нии х1 от главного фокуса F положительной оптической
системы. Изображение предмета имеет размер у1. Линей-
Изображение предмета имеет размер у1. Линей-
ное увеличение в1 равно
(4)
1
1
x
f
y
y β = =
Если теперь отодвинуть предмет от линзы на рас-
стояние Δх, то линейное увеличение в2 окажется равным
2
2
2 x
f
y
y β = = (5)
Из (4) и (5) нетрудно получить
1 2
1 1
β − β
Δ
f = x , (6)
где Δх = x2 — x1 — перемещение предмета.
Таким образом, для определения фокусного рас-
стояния толстой положительной линзы нужно измерить
линейное увеличение системы при двух положениях
предмета и расстояние между этими двумя положения-
ми.
Для нахождения главных плоскостей системы не-
достаточно знать фокусное расстояние, нужно опреде-
лить ещё положения главных фокусов. Это можно сде-
лать при помощи зрительной трубы, настроенной на
бесконечность. Отложив от главных фокусов отрезки,
равные фокусному расстоянию, можно найти положе-
ния главных плоскостей системы. Теоретически фокус-
ное расстояние f/сложной системы, состоящей из двух
тонких положительных линз, можно рассчитать (см.
[1]), если известны фокусные расстояния каждой линзы
и расстояние между их центрами l12:
| |
1 1 1 | |
/
2
/
1
12
/12 /
/ f f
l
f f f
= + − (7)
Экспериментальная установка. Оптическая ска-
мья с осветителем, набор линз, экран и зрительная
труба позволяют определить параметры оптических
систем всеми описанными способами. Все оптические
элементы устанавливаются на скамье при помощи рей-
теров.
Важную роль играет правильная центрировка
элементов системы. Проходя через плохо отцентриро-
ванную систему, лучи света могут отклониться и прой-
ти мимо экрана или глаза наблюдателя. Центрировать
линзы следует как по высоте, так и в поперечном на-
правлении (для чего линзы установлены на поперечных
салазках). Подробно с правилами центрировки системы
Вы познакомитесь при выполнении задания.предмет лежит слева от передней главной плоскости, а2 положительно, если изображение лежит справа от задней плоскости, а фокусное расстояние f берётся со своим знаком. Следует подчеркнуть, что главные плоскости и главные точки могут лежать как внутри, так и вне системы и при этом могут располагаться асимметричноотносительно поверхностей, ограничивающих оптическую систему. Большой практический интерес представляет случай, когда размер оптической системы в направле нии главной оптической оси значительно меньше фокусного расстояния. Оптический луч, проходя внутри такой системы, мало смещается, поэтому главные плоскости Р1 и Р2(рис. 2) практически совпадают и располагаются где-то посередине системы . Такая оптическая система называется тонкой линзой. Формула (1) остаётся, конечно, справедливой и для тонкой линзы; расстояния a1 и a2 и фокусное расстояние f можно в этом случае приближённо отсчитывать от центра линзы.
Следует подчеркнуть, что главные плоскости и главные точки могут лежать как внутри, так и вне системы и при этом могут располагаться асимметричноотносительно поверхностей, ограничивающих оптическую систему. Большой практический интерес представляет случай, когда размер оптической системы в направле нии главной оптической оси значительно меньше фокусного расстояния. Оптический луч, проходя внутри такой системы, мало смещается, поэтому главные плоскости Р1 и Р2(рис. 2) практически совпадают и располагаются где-то посередине системы . Такая оптическая система называется тонкой линзой. Формула (1) остаётся, конечно, справедливой и для тонкой линзы; расстояния a1 и a2 и фокусное расстояние f можно в этом случае приближённо отсчитывать от центра линзы.
I. Определение фокусного расстояния тонкой положительной линзы.
Фокусные расстояния тонких положительных линз можно определять различными способами. Как было выяснено выше, в «приближении тонкой линзы» считается, что обе главные плоскости совпадают и проходят через середину линзы. Отсчитывая расстояния от середины линзы до предмета и до изображения, мы допускаем ошибку порядка толщины стекла. При необходимости получить более точные значения f приходится отбросить «приближение тонкой линзы» и учитывать расстояние д междуглавными плоскостями.
Отсчитывая расстояния от середины линзы до предмета и до изображения, мы допускаем ошибку порядка толщины стекла. При необходимости получить более точные значения f приходится отбросить «приближение тонкой линзы» и учитывать расстояние д междуглавными плоскостями.
Способ 1. Фокусное расстояние тонкой положительной линзы можно определить, исходя из формулы линзы. Для этого достаточно измерить расстояния а1 и а2 (рис.2), полагая д → 0, и затем вычислить f по формуле (1). Проведя измерения при увеличенном и при уменьшенном изображении (рис.3), а также при различных положениях предмета и изображения, можно найти среднее значение фокусного расстояния.
Точность определения фокусного расстояния по формуле линзы зависит от расстояния между предметом и изображением. Используя соотношение (1), самостоятельно решите вопрос, какое положение предмета и экрана позволяет получить наиболее точное значение f.
Способ 2. Фокусное расстояние тонкой положительной линзы можно определить с помощью зрительной трубы, настроенной на бесконечность, то есть на параллельный пучок лучей.
Разместив между предметом и зрительной трубой положительную линзу и перемещая её вдоль оси системы, можно найти резкое изображение предмета в окуляре зрительной трубы. При этом
расстояние от середины линзы до предмета равно фокусному расстоянию тонкой линзы. Для толстой линзы зрительная труба позволяет определить только положение главного фокуса.
II. Определение фокусного расстояния тонкой отрицательной линзы
Способ 1. Определение фокусного расстояния отрицательной линзы затруднено тем, что изображение предмета получается мнимым (при действительном источнике) и поэтому не может быть
получено на экране. Эту трудность легко обойти с помощью вспомогательной положительной линзы. Сначала с помощью положительной линзы получают на экране действительное изображение
предмета S (точка S1 на рис. 4). Затем на пути лучей, выходящих из положительной линзы, располагают исследуемую отрицательную линзу и, отодвигая экран, получают четкое изображение предмета на экране, отрицательной линзы, образованное двумя линзами. Точка S1 пересечения сходящихся лучей играет по отношению к отрицательной линзе роль мнимого источника. Изображение источника переместится теперь в точку S2.
Точка S1 пересечения сходящихся лучей играет по отношению к отрицательной линзе роль мнимого источника. Изображение источника переместится теперь в точку S2.
Определив расстояния а1 (а1 = а0— l) и а2, рассчитывают фокусное расстояние рассеивающей линзы по формуле (1).
С п о с о б 2. Если расстояние а1 (рис. 4) совпадает с фокусным расстоянием отрицательной линзы, то изображение перемещается в бесконечность, т. е. лучи выходят из линзы параллельным пучком.
Параллельность пучка можно установить с помощью зрительной трубы, настроенной на бесконечность. Зная расстояние от первой линзы до точки S1 и расстояние между линзами, нетрудно определить фокусное расстояние тонкой отрицательной линзы. Для толстой отрицательной линзы этот метод позволяет определить только положение главного фокуса.
III. Определение фокусного расстояния и положения главных плоскостей сложной оптической системы.
Ни один из описанных выше способов не позволяет определить фокусное расстояние и положение
главных плоскостей толстой линзы, т.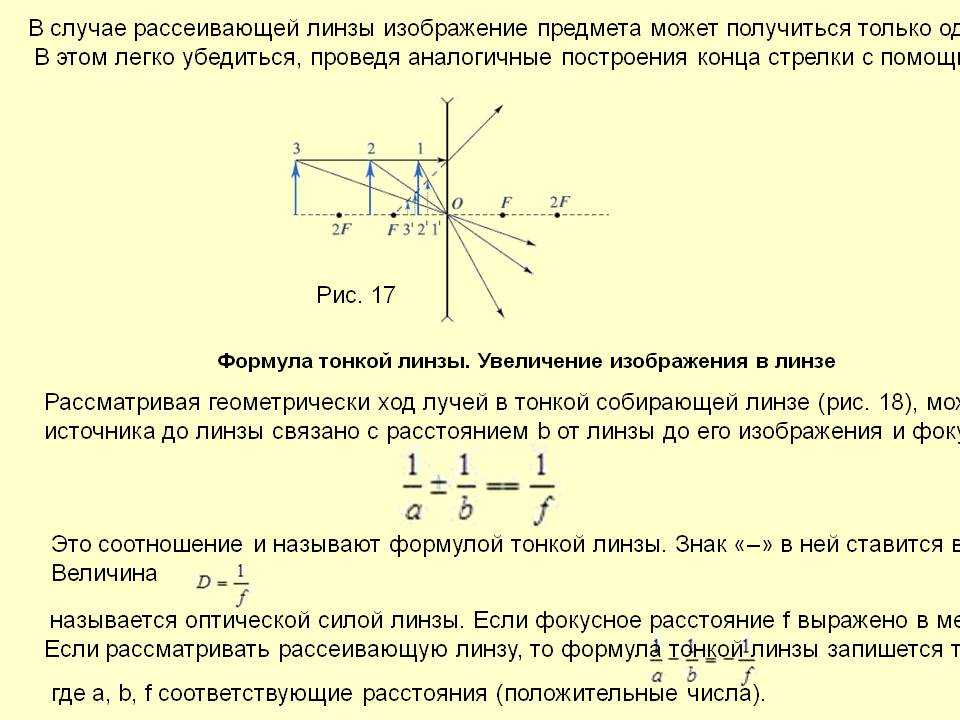 е. такой оптической системы, толщина которой не мала по сравнению сфокусным расстоянием.
е. такой оптической системы, толщина которой не мала по сравнению сфокусным расстоянием.
ЗАДАНИЕ
В этом упражнении предлагается определить фо-
кусные расстояния тонких собирающих и рассеивающих
линз, рассчитать их светосилу и оптическую силу, а
также определить фокусное расстояние и положения
главных плоскостей сложной оптической системы.
I. Центрировка элементов оптической системы
1. Держа линзу в одной руке, получите на ладони
другой руки изображение любого удалённого объекта
(окна, лампочки) и оцените на глаз фокусное расстоя-
ние линзы. Линза, которая не даст действительного
изображения, — рассеивающая. Запишите приближён-
ные значения фокусных расстояний.
2. Соберите и отцентрируйте установку. Для этого
на одном конце оптической скамьи установите освети-
тель с ирисовой диафрагмой (предмет) и вплотную к
нему экран на рейтере. Отрегулируйте высоту экрана
так, чтобы его центр совпадал с центром яркого кругло-
го пятна от осветителя. Эта операция должна выпол-
Эта операция должна выпол-
няться при плотно затянутом винте, закрепляющем рей-
тер на оптической скамье. Для перемещения рейтера
вдоль скамьи винт следует только слегка ослабить, что-
бы не допустить перпендикулярного скамье смещения
центра. Перемещая рейтер, прижимайте его к скамье со
стороны, противоположной винту.
3. Отодвиньте экран от осветителя и разместите
в промежутке рейтер с собирающей линзой № 1. Пере-
двигая линзу и экран вдоль скамьи, добейтесь чёткого
изображения края ирисовой диафрагмы осветителя на
экране. Закрепите рейтеры. Смещая линзу с помощью
поперечных салазок и по высоте, приведите центр изо-
бражения к центру экрана.
4. Оптические оси линз устанавливаются парал-
лельно ребру оптической скамьи на глаз. Легко убе-
диться на опыте, что при небольших увеличениях, по-
лучаемых в настоящей работе, такая установка является
достаточной.
5. Остальные линзы можно отцентрировать позд-
нее. Для центрировки рассеивающих линз следует вос-
пользоваться уже отцентрированной положительной
линзой, расположив её впереди отрицательной. Способ
Способ
центрировки рассеивающих линз продумайте самостоя-
тельно.
II. Определение фокусных расстояний тонких
линз при помощи экрана
(Измерения проводятся для одной положительной и
одной отрицательной линзы.)
1. Установите положительную линзу № 1 между
осветителем и экраном. Расположите экран на расстоя-
нии L > 4f от предмета (рис. 3). Перемещая линзу вдоль
скамьи, получите увеличенное и уменьшенное изоб-
ражения предмета (края ирисовой диафрагмы) на экра-
не. Посмотрите, как влияют на чёткость изображения
размер диафрагмы и яркость источника.
2. С помощью линейки измерьте расстояния от
линзы до предмета и до изображения (а1, а2, а/
1, а/
2 на
рис. 3). Середина линзы и положение ирисовой диа-
фрагмы отмечены на оправах проточками.
3. При фиксированном расстоянии между осве-
тителем и экраном, слегка перемещая линзу, повторите
измерения несколько раз.
4. Независимо измерьте расстояние L от предмета
до экрана и перемещение линзы (рейтера) l. При фикси-
При фикси-
рованном значении L измерьте перемещение l несколь-
ко раз.
5. По результатам измерений определите среднее
формулу (1), а затем формулу (3).
6. Для определения фокусного расстояния тонкой
отрицательной линзы используйте вспомогательную по-
ложительную линзу. Сначала с помощью ко-
роткофокусной положительной линзы получите на эк-
ране увеличенное изображение предмета и измерьте
линейкой расстояние от линзы до экрана (ао на рис. 4).
Затем между положительной линзой и экраном раз-
местите рассеивающую линзу и, отодвигая экран от
линзы, найдите действительное изображение предмета,
образованное системой линз. Измерьте расстояние a2 от
рассеивающей линзы до экрана и расстояние между
линзами /.
Рассчитайте величину а1 и определите фокусное
расстояние рассеивающей линзы с помощью формулы
(1). При вычислении фокусного расстояния нужно при-
писать величинам а1 и а2 правильные знаки (а1 < О, а2>
0).
III. Определение фокусных расстояний тонких
линз с помощью зрительной трубы
(Измерения проводятся для двух положительных
и одной отрицательной линзы.)
1. Для определения фокусных расстояний линз с
помощью зрительной трубы необходимо настроить тру-
бу на бесконечность. Эту настройку проще всего осуще-
ствить, наведя трубу на удалённый объект (например,
на окно в конце длинного коридора). Предварительно
вращением глазной линзы окуляра трубы настройтесь
на резкое видение окулярной шкалы (если окулярная
шкала отсутствует, то совместите штрих на глазной лин-
зе с точкой на тубусе). Не следует настраивать трубу на
предмет, расположенный за оконным стеклом, т. к.
оконное стекло часто оказывается недостаточно пло-
ским.
2. Поставьте положительную линзу на расстоя-
нии от предмета, примерно равном фокусному. На не-
большом расстоянии от линзы закрепите трубу, настро-
енную на бесконечность, и отцентрируйте её по высоте.
Передвигая линзу вдоль скамьи, сначала получите в
окуляре зрительной трубы изображение поверхности
матового стекла; затем, перемещая линзу с помощью
поперечных салазок и меняя диаметр светового пятна с
помощью ирисовой диафрагмы, настройтесь на чёткое
изображение края диафрагмы. При этом расстояние
между предметом и серединой тонкой линзы (между
проточками на оправах) равно фокусному.
3. Поверните линзу другой стороной к источнику
и повторите измерения фокусного расстояния. По результатам измерений сделайте вывод, можно ли считать линзу тонкой.
4. Измерьте фокусное расстояние второй тонкой положительной линзы при помощи зрительной трубы.
5. Для определения фокусного расстояния тонкой отрицательной линзы используйте схему, изображённую на рисунке 4. Сначала получите на экране увеличенноеизображение диафрагмы при помощи короткофокуснойположительной линзы, затем измерьте расстояние аомежду линзой и экраном.
Разместите сразу за экраном трубу, настроенную на бесконечность, и закрепите её. Уберите экран и поставьте на его место исследуемую рассеивающую линзу. Отцентрируйте световой пучок с помощью листа бумаги. Перемещая рассеивающую линзу, найдите в окуляре зрительной трубы резкое изображение краядиафрагмы.
Уберите экран и поставьте на его место исследуемую рассеивающую линзу. Отцентрируйте световой пучок с помощью листа бумаги. Перемещая рассеивающую линзу, найдите в окуляре зрительной трубы резкое изображение краядиафрагмы.
Если изображение недостаточно чёткое, задиафрагмируйте положительную линзу и заново проведитезначение фокусного расстояния, используя сначаланастройку с экраном (диафрагма диаметром 1 смуменьшит сферические аберрации и повысит чёткостьизображения). Подберите оптимальную яркость источника.
Измерив расстояние между линзами l, рассчитайте фокусное расстояние рассеивающей линзы: f’ = ао — l.
6. Поверните рассеивающую линзу другой стороной к источнику и повторите измерения.
7. Сравните результаты определения фокусныхрасстояний и оцените случайные ошибки измерений.
При значительном расхождении результатов попытайтесь понять причину расхождения.
8. Определите, какая из линз обладает наибольшей светосилой, какая наибольшей оптической силой (диоптрийностью).
IV. Определение фокусного расстояния сложной оптической системы
1. Для создания сложной оптической системы установите в центре оптической скамьи две тонкие соби-
рающие линзы на расстоянии, в полтора-два раза превышающем сумму их фокусов, и закрепите рейтеры. Измерьте расстояние l12 между линзами.
2. Для определения фокусного расстояния системы по формуле (6) расположите экран на дальнем конце скамьи.
Установите на осветителе диафрагму диаметром 1 см (по риске на оправе осветителя) и, перемещая осветитель вдоль скамьи, получите на экране резкое изображение диафрагмы. Измерьте расстояние от диафрагмы до первой линзы и величину
изображения у1(см. рис. 5).
Отодвиньте источник на несколько сантиметров от прежнего положения и, передвигая экран, вновь получите резкое изображение диафрагмы.
Для повышения точности размеров изображений у1 и у2 должны заметно отличаться друг от друга.
Измерив расстояние от предмета до первой линзы и рассчитав перемещение Δх, определите фокусное расстояние системы по формуле (6).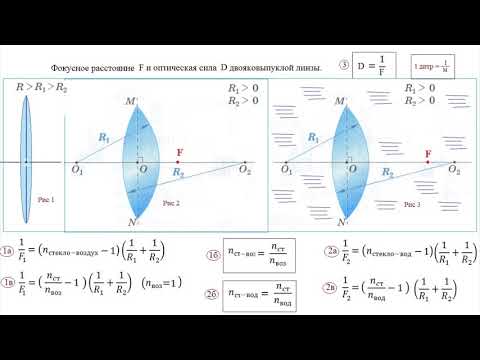
3. Для нахождения положения главных фокусов системы закрепите зрительную трубу за второй линзой, подвиньте осветитель к первой линзе иотцентрируйте систему с помощью листа бумаги.
Медленно отодвигая осветитель от системы, сначала найдите резкое изображение поверхности стекла в окуляре зрительной трубы, а затем, последовательно уменьшая размер пятна и перемещая пятно с помощью винта поперечных салазок линзы, настройтесь на край ирисовой диафрагмы.
Для точной настройки задиафрагмируйте пер-ую линзу и подберите подходящую яркость пучка.
Определите положение переднего главного фокуса системы, измерив расстояние Д от предмета до первой линзы.
4. Поменяйте линзы местами и повторите измерения п. 3, сохранив неизменным расстояние между линзами.
5. На миллиметровой бумаге постройте в масштабе чертёж оптической системы. Укажите на нём положения фокусов каждой из линз.
Постройте ход луча, вошедшего в систему слева параллельно главной оптической оси, последовательно через каждую из линз. Точка пересечения луча, вышедшего из системы, с оптической осью определяет положение одного из главных фокусов системы (F2 на рис. 1). Определите расстояние Δ от него до ближайшей линзы.
Точка пересечения луча, вышедшего из системы, с оптической осью определяет положение одного из главных фокусов системы (F2 на рис. 1). Определите расстояние Δ от него до ближайшей линзы.
очка пересечения вышедшего луча с продолжением входящего определяет положение задней главной плоскости системы (Р2). Расстояние от точки Н2 пересечения задней главной плоскости с оптической осью до заднего главного фокуса F2 равно фокусному расстоянию системы.
6. Повторите построение для луча, вошедшего в систему справа и сравните определённые графически величины Δ с экспериментальными, а величины фокусных расстояний — с расчётами поформулам (6) и (7).
Контрольные вопросы
1. Рассмотрев ход лучей на рисунке 2, полчите формулу Ньютона:
2. Дайте определения главных фокусов, фокусных расстояний и главных плоскостей сложной центрированной оптической системы.
3. Дайте определения оптической силы и светосилы линзы.
4. Покажите, что если расстояние между предметом и экраном превышает 4, то изображение на экране может быть получено при двух различных поло-
жениях линзы.
5. Нарисуйте главные плоскости системы, состоящей из двух тонких линз — положительной и отрицательной, с известными фокусными расстояниями.
ЛИТЕРАТУРА
1. Сивухии Д.В. Общий курс физики. Оптика. М.: Наука, 1980. Т. IV. Гл. II.§9-16.
2. Лаидсберг Г.С. Оптика. М.: Наука, 1976. Гл. XII, § 71-73, 75 79; гл. XIII, § 80-82, 86.
3. Годжаев Н.М. Оптика. М.: Высшая школа, 1977. Гл. VII, §2, 4-6.
4. Дитчберп Р. Физическая оптика. М.: Наука, 1965. Гл. 7.
Средний рейтинг
Еще нет оценок
Вам нужно авторизироваться для того, чтобы проголосовать.
Автоколлиматор | Измерение фокусного расстояния линзы
+7 (495) 781 39 39
Главная/Контрольно-измерительное оборудование/OEG/Измерение фокусного расстояния линзы
Оптические измерительные установки фирмы OEG, широко применяемые во всём мире, являются проверенным решением проблемы измерения оптических параметров отдельных линз и оптических систем
| Уникальная концепция фирмы OEG обеспечивает высочайшую точность измерений. Высокая степень автоматизации моторизированных перемещений и обработки измерительной информации обеспечивается программным обеспечением, разработанным фирмой OEG. Установки обеспечивают измерение следующих параметров для сферической оптики: — Измерение фокусного расстояние линзы:
— Радиус R (Р) OTS может быть доукомплектованa для измерения плоской оптики. Базовая конфигурация
Автоколлиматор измерительной головки может быть использован, в зависимости от функции измерения, в режиме автоколлимации или как телескоп (в сочетании с измерительным коллиматором). Элементы подсветки оснащены электронным регулятором яркости с целью корректировки отражающих характеристик измеряемого объекта (используя автоколлимацию) или свободной апертуры измеряемой линзы (измерения в проходящем свете). Типы OTS
Базовые функции измерения Измерение ошибки центрирования MTF измерение Измерение плоской оптики Измерение цилиндрической оптики 1. Измерение симметрии (смещения) 2. Измерение изгиба 3. Измерение угла оси цилиндрической линзы |
Специальные решения для тестирования оптики и камер
На базе нашего стандартного оборудования мы можем разрабатывать специальные решения в краткие сроки и по доступным ценам. Снимок справа показывает специальную систему высокоточной регулировке ПЗС-матриц в промышленных камерах (имеется специальная информация о продукте). Эта система также подходит для бесконтактного измерения ГФР, радиуса и высоты объектов.
Снимок справа показывает специальную систему высокоточной регулировке ПЗС-матриц в промышленных камерах (имеется специальная информация о продукте). Эта система также подходит для бесконтактного измерения ГФР, радиуса и высоты объектов.
Другими решениями, уже реализованными на заказ для нескольких клиентов, являются измерение камеры MTF или специальных стендовых регулировок для датчиков по критериям MTF. Разумеется, специализированные стендовые регулировки МТФ, как MTF ВАРИАНТ или MTF МАСТЕР являются компонентами нашего стандартного оборудования. Для этих продуктов имеется специальная информация.
Схемы измеренийИзмерение фокусного расстояния линзы (EFL) |
Измерение EFL. Результат измерения фокусного расстояния линзы — в окне Focal lenght. EFL пропорционально расстоянию между штрихами на видеоизображении. Автофокусирование обеспечивает очень высокую повторяемость измерений. |
| Результаты измерений могут быть представлена в форме текста.Оператор может организовать удобную форму протокола. |
Измерение фокусного расстояния – измерение заднего фокусного расстояния (BFL)
Под BFL понимается расстояние межу вертексом крайней линзы и сенсором. Все действия выполняются автоматически. Благодаря автофокусированию, достигается высокая повторяемость и объективность измерения. |
Измерение радиуса поверхности линзы
Измерение центрирования линзМодуль хе входит в комплект поставки
Измерительный модуль |
+7 (495) 781 39 39
107023, г. Москва, ул. Электрозаводская, д.24,
стр.3, оф. В303
Copyright © 2007 — 2021 ООО «БЛМ Синержи»
Мегагрупп.ру
Фокусное расстояние линз | Сайн Сервис — Статьи
Новости
Луч CO2лазера, формируемый лазерной трубкой, преломленный зеркалами, напрямую фокусируется на заготовке, с помощью фокусирующей линзы. Для процесса лазерной резки необходимо сфокусировать лазерный луч высокой мощности в пятно минимального диаметра, которое имеет необходимую плотность мощности для осуществления резания. Фокусное расстояния фокусирующей линзы определяет диаметр пятна и глубину фокуса — эффективное расстояние, в пределах которого достигается максимальное качество резки.
Фокус лазерного луча изображена ниже, где 2×z глубина фокуса (Длина Рэлея), диаметр фокусируемого пятна df имеет зависимость:
df = 4λ/π×f/D×1/K = 4λ/π×f/D×M2
Зависимость показывает, что фокусируемое пятно лазерного луча минимального диаметра достижимо при меньшем фокусном расстоянии (f), хорошем качестве луча, имеющим параметр K близкий к 1 (M2=1/K), большом диаметре параллельного лазерного луча на фокусирующей линзе (D) и короткой длине волны (λ). Глубина фокуса также зависит от тех же параметров, что и диаметр пятна. Как правило, чем меньше диаметр фокусируемого лазерного луча, тем меньше глубина фокуса.
Глубина фокуса также зависит от тех же параметров, что и диаметр пятна. Как правило, чем меньше диаметр фокусируемого лазерного луча, тем меньше глубина фокуса.
Для лазерной резки тонких материалов (толщиной менее 4 мм) небольшое фокусное расстояние, в среднем 63,5 мм, на практике обеспечивает узкий прорез и гладкую поверхность кромки за счет минимального диаметра фокусируемого лазерного луча. Большое фокусное расстояние предпочтительно при резке толстых материалов, где глубина фокуса должна быть приблизительно равна половине толщины заготовки. Лазерный луч с высоким качеством должен обеспечивать большое фокусное расстояние без увеличения диаметра фокусируемого пятна. Диаметр фокусируемого пятна и глубина фокуса это параметры, определяющие фокусное расстояние, которое оптимизируется в зависимости от толщины обрабатываемого материала.
На практике нам часто нужно рассчитать какую толщину материала может прорезать линза с идеально прямым резом, в таком случае нам поможет формула:
2z= 2.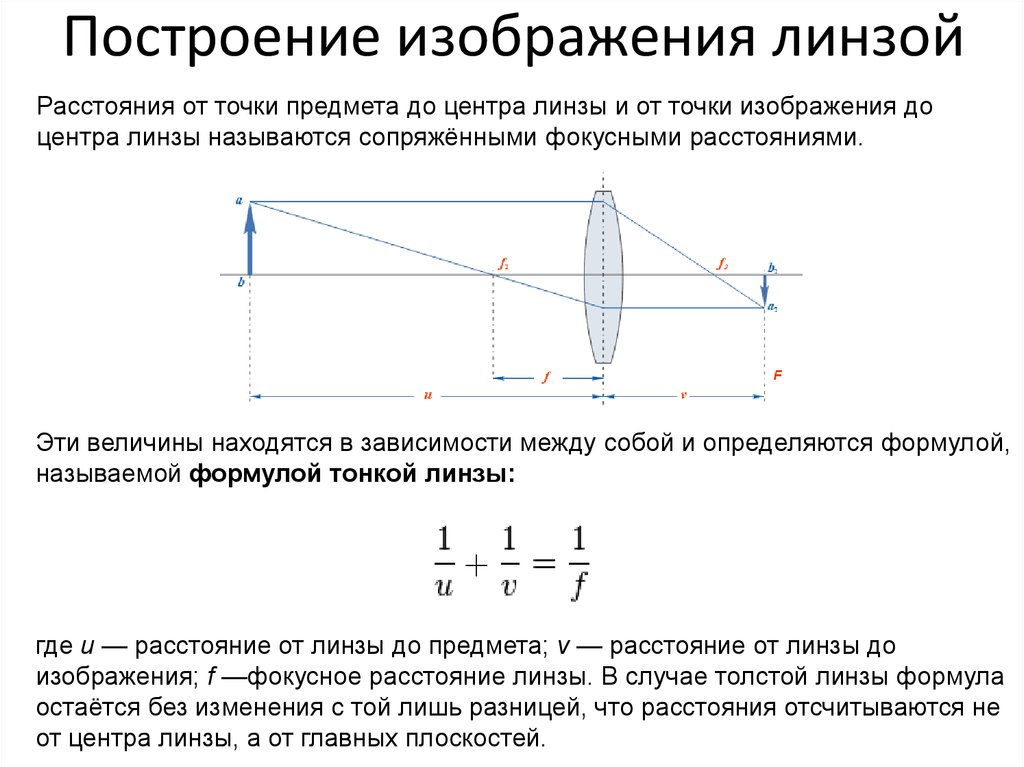 2 = 2,8 мм
2 = 2,8 мм
Еще раз оговоримся, что это НЕ максимальная толщина материала, которую можно прорезать определенной линзой. Она прорежет гораздо большую толщину и какую толщину можно прорезать определяет не линза, а мощность излучателя. Это та толщина, при которой рез будет идеально прямым, так как при большей толщине материала углы краев реза начнут скругляться. Например, при увеличении толщины материала на 30%, это скругление не будет заметно глазу, поэтому например на 5″ линзах многие режут и 15 мм, а кого-то устраивает и форма реза даже на 20 мм толщины материала.
© 2017 САЙН СЕРВИС. Все права защищены.
Любое копирование информации с сайта sign-service.ru должно производится с сылкой на источник и с согласия администрации ресурса.
Читайте также
Новости
Механика для широкоформатных принтеров
Независимо от того, какой принтер у вас, подобные устройства не вечны.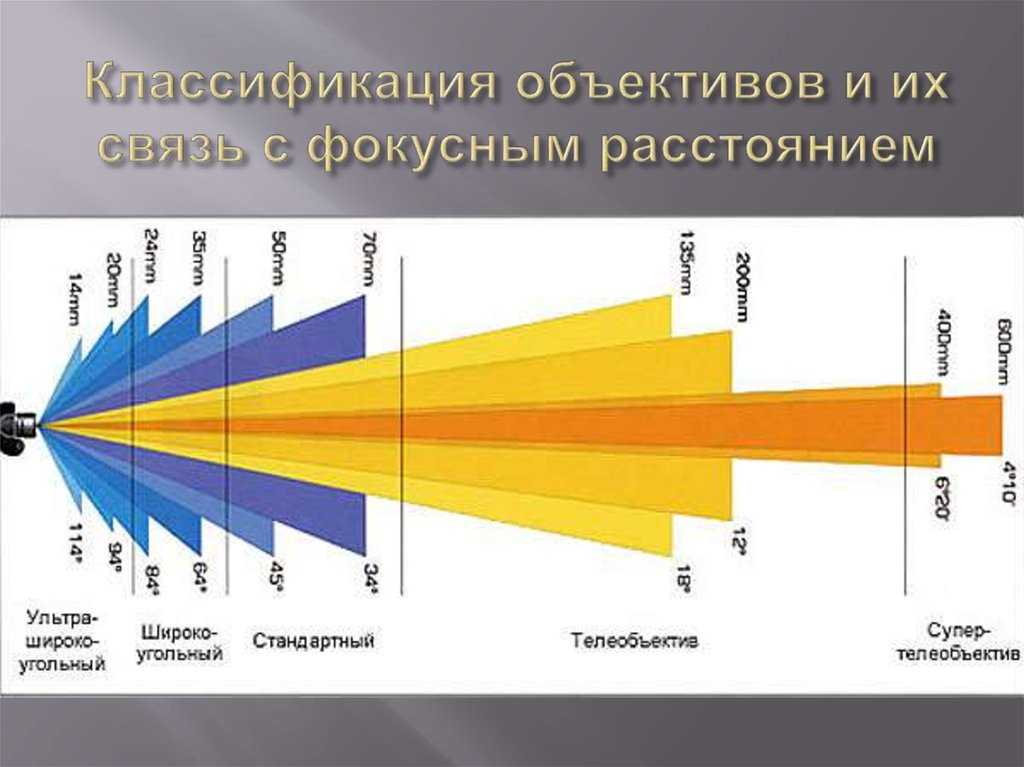 Как результат перегрева, повышенной эксплуатации, механических повреждений, или естественного износа, такое оборудование может выйти из строя. Особенно это касается механики оборудования. Мы предлагаем вашему вниманию широкий выбор различных деталей, с помощью которых можно отремонтировать ваш принтер.
Как результат перегрева, повышенной эксплуатации, механических повреждений, или естественного износа, такое оборудование может выйти из строя. Особенно это касается механики оборудования. Мы предлагаем вашему вниманию широкий выбор различных деталей, с помощью которых можно отремонтировать ваш принтер.
Читать
Новости
Плоттерная резка и фрезерование на планшетном плоттере
Использование при производстве различных изделий планшетной резки открывает новые горизонты развития для фирмы. Новая технология позволяет оказывать совершенно новые услуги и работать с новыми материалами. Чем шире перечень операций, которые может выполнять станок, тем шире горизонты развития компании.
Читать
Новости
Как правильно выбрать и купить фрезерный станок
Для запуска производства необходимо правильно подобрать и приобрести оборудование, на котором будут выполняться все работы. Независимо от того, что именно вы собираетесь выпускать, главной покупкой для запуска производства является фрезерный станок.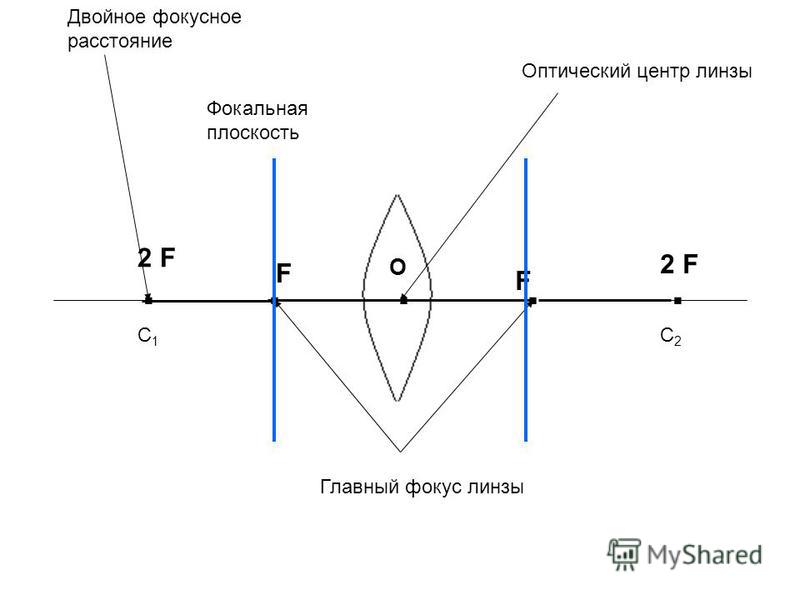
Читать
Новости
Фрезерный станок – оборудование для изготовления рекламной продукции
Облик современных городов преобразился кардинально: он стал ярче и наряднее, особенно хорошо эти изменения заметны в темное время суток. Такое преображение стало возможным благодаря обилию рекламы: рекламные щиты, лайтбоксы и рекламные вывески – все это не только изменяет облик города, но и влияет на потребление людей, формирует предпочтения.
Читать
Новости
Направляющие лазерного гравера: назначение и основные виды
В последние годы развитие технологий привело к тому, что когда-то дорогостоящее оборудование сегодня может себе позволить каждый желающий. Это утверждение в полной мере относится и к лазерному граверу. Данное устройство с успехом используется как в профессиональной среде, так и иногда в домашних условиях.
Читать
Последние новости
Технологичное оборудование для изящной работы с металлом
Обзор интерьерных принтеров
Как выбрать и купить шпиндель для станка ЧПУ
Режущий плоттер – основа производства рекламной продукции
Фрезерные станки: особенности конструкции
Как использовать термопресс для кружек?
Как рассчитать фокусное расстояние объектива: немного упрощенно
Последние пару дней я участвовал в интересном обмене идеями с Тони Нортрапом об эффективном фокусном расстоянии объектива Canon 70-200mm f/2. 8L IS II. объектива, когда он сфокусирован на расстояния, меньшие, чем его установка на бесконечность (т. е. фокусировка дышит). Мы придумывали совершенно разные цифры (мои были представлены в видеоролике в прошлом месяце), и у нас не так много внешних источников, чтобы проверить себя… возможно, потому, что расчет — не очень простой процесс. Итак, если у вас когда-либо возникало желание увидеть, как на самом деле работают ваши линзы или как сильно они дышат, вот как я это делаю, используя несколько инструментов, которые я использую, чтобы сделать это быстрее. Большая часть этого была заимствована из сообщения на форуме StackExchange пользователем «Вивек» на основе метода Боба Аткинса, поэтому вы можете проверить это для получения дополнительной информации. Мне было бы интересно услышать ваши измерения для этого объектива, в частности, на расстоянии от 5 до 12 футов от объекта.
8L IS II. объектива, когда он сфокусирован на расстояния, меньшие, чем его установка на бесконечность (т. е. фокусировка дышит). Мы придумывали совершенно разные цифры (мои были представлены в видеоролике в прошлом месяце), и у нас не так много внешних источников, чтобы проверить себя… возможно, потому, что расчет — не очень простой процесс. Итак, если у вас когда-либо возникало желание увидеть, как на самом деле работают ваши линзы или как сильно они дышат, вот как я это делаю, используя несколько инструментов, которые я использую, чтобы сделать это быстрее. Большая часть этого была заимствована из сообщения на форуме StackExchange пользователем «Вивек» на основе метода Боба Аткинса, поэтому вы можете проверить это для получения дополнительной информации. Мне было бы интересно услышать ваши измерения для этого объектива, в частности, на расстоянии от 5 до 12 футов от объекта.
Я также хотел бы услышать ваши результаты использования другой методологии и ваши объяснения этих методов.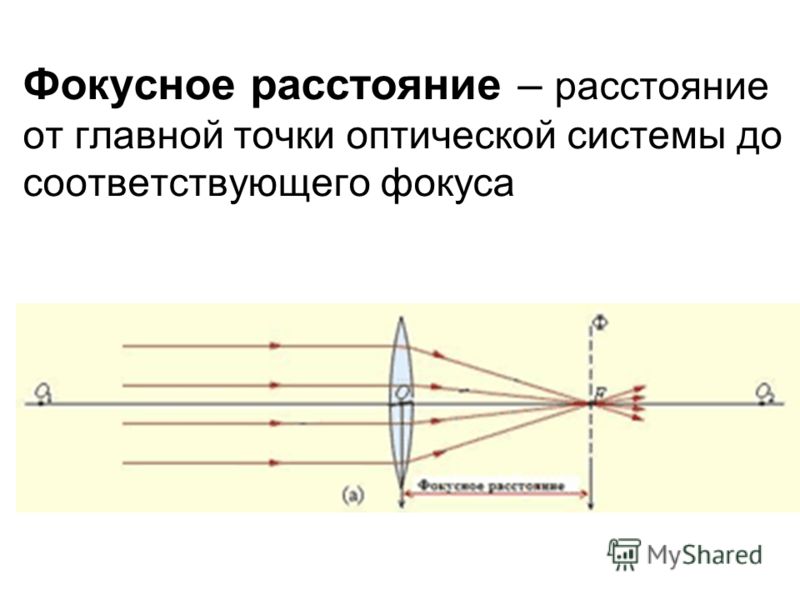 Было бы здорово, если бы я мог найти метод тестирования, который был бы проще этого и был бы таким же точным или лучше.
Было бы здорово, если бы я мог найти метод тестирования, который был бы проще этого и был бы таким же точным или лучше.
Настройка
Для начала установите камеру на штатив возле стены или другой вертикальной поверхности. Измерьте расстояние от центра сенсора камеры до пола (можно использовать вертикальный центр крепления объектива). Мы назовем это H . Затем прикрепите что-то вроде метрической линейки (или метрической измерительной ленты, в зависимости от ширины объектива) вертикально к стене, нижним концом точно на высоте центра сенсора вашей камеры от пола (H). Это просто для установки квадратного угла треугольника. Также важно убедиться, что камера выровнена по линейке вертикально.
После этого сфокусируйте среднюю точку фокусировки на конце линейки. Поскольку ваша точка автофокусировки, скорее всего, представляет собой прямоугольник, конец линейки должен делить его пополам, деля пополам (если шкала вашей линейки не начинается прямо на конце линейки, то центрируйте первые отметки на шкале в центр точки автофокусировки).
Расстояние от датчика до объекта
Измерьте расстояние от крепления объектива камеры до стены/линейки в миллиметрах. Мне нравится использовать точную лазерную измерительную ленту. Мой Bosch GLM 50 имеет точность около 1,5 мм, но некоторые другие даже лучше. Если вы будете осторожны и у вас есть помощь, рулетка тоже подойдет, хотя и с меньшей точностью.
Рис. 1. Зеленая стрелка указывает на маркер фокальной плоскости камеры.Добавьте к вашему измерению FFD (фокусное расстояние фланца). Это FFD для наиболее распространенных брендов, но больше можно найти в Википедии:
- Canon EF/EF-S: 44 мм
- Nikon F: 46,5 мм
- Микро 4/3 : 19,25 мм
- Fuji X: 17,7 мм
- Sony E: 18 мм
В качестве альтернативы вы можете измерить от маркера фокальной плоскости на вашей камере, если он есть. Если вы это сделаете, это будет выглядеть как значок на рисунке 1 . Лично мне проще получить точные и воспроизводимые измерения с помощью крепления объектива, но это на ваше усмотрение.
Мы назовем это измерение х .
Измерение по вертикали
Теперь сфокусируйте камеру и сделайте снимок. Если ваша установка не является полностью жесткой, сделайте несколько снимков, чтобы убедиться, что точный центр изображения находится над концом шкалы линейки.
Затем загрузите изображение в Photoshop. Создайте горизонтальную направляющую на 50%. Эта линия должна совпадать с началом шкалы линейки на изображении. Отсюда все просто: посмотрите на верхнюю границу изображения и прочитайте, где линейка выходит из рамки. Это измерение является противоположной стороной треугольника, которую мы назовем 9.0005 Д .
Чтение длины этой линейки на вашем изображении дает вам «Y» Если эта направляющая не совпадает с началом шкалы линейки, отрегулируйте камеру и повторите съемку или, если вам удобно пользоваться линейкой инструмент в Photoshop, определите, насколько далеко направляющая находится от начала шкалы, и добавьте или вычтите это значение. Вы можете не использовать инструмент линейки или делать оценки, центрируя точку автофокусировки на отметке 10 см, а не на самом конце, а затем вычитая 100 мм (плюс или минус) из вашего окончательного измерения, но поскольку это добавляет еще одну возможность для ошибок подкрадываться к процессу, я предпочитаю начинать с 0.
Вы можете не использовать инструмент линейки или делать оценки, центрируя точку автофокусировки на отметке 10 см, а не на самом конце, а затем вычитая 100 мм (плюс или минус) из вашего окончательного измерения, но поскольку это добавляет еще одну возможность для ошибок подкрадываться к процессу, я предпочитаю начинать с 0.
Вычислите угол
Если вы помните свою геометрию, это довольно просто, но еще проще использовать онлайн-калькулятор, такой как этот на EasyCalculation.com.
Настройте выпадающие меню так, чтобы он вычислял угол и сторону гипотенузы, хотя нам нужен только угол.
В поля ниже введите размер по оси X для соседней стороны и размер по оси Y для противоположной стороны и нажмите «Рассчитать». Это даст вам угол, который нам нужен. Мы назовем это А .
Расчет фокусного расстояния
Формула для расчета фокусного эффективного фокусного расстояния: f = d / (2 * tan(α/2)) , где…
f= фокусное расстояние
d= размер по вертикали датчика в миллиметрах
(α/2) = угол, который мы рассчитали выше. Обратите внимание, что угол выше ( A ) заменяет все это выражение, а не только «α».
Обратите внимание, что угол выше ( A ) заменяет все это выражение, а не только «α».
Итак, если вы рассчитываете фокусное расстояние с помощью полнокадровой камеры с датчиком 36 x 24 мм, уравнение должно выглядеть так:
f = 24 / (2 * tan(A))
Например, если мы вычислили угол A равным 3,22 градуса. Тогда:
f = 24/(2 * тангенс (3,22 градуса))
Итак, как это решить? Самый простой способ — отдать его Wolfram Alpha. Просто скопируйте и вставьте его. Он определит значение f, а f = ваше фокусное расстояние, в данном случае это 213,3 мм . [Обновление: как указал Билл Минтон, вы можете так же легко вставить это в Google, и он также решит для фокусного расстояния].
Кстати, если вы не наберете слово «градусы» или не используете соответствующий символ, Wolfram Alpha рассчитает ответ в радианах, а не в градусах, и ответ будет выглядеть странно. Однако это даст вам возможность в поле с надписью «Предполагая, что «загар» — это математика…», вместо этого переключиться на градусы.
Визуальный: За последнюю неделю я искал несколько разных способов перепроверить свои измерения и убедиться, что то, что я получаю, имеет смысл. Если вы видели мое видео-сравнение объективов Canon и Tamron и их дыхания, то вы видели отрывок из видео Мэтта Грейнджера на эту тему, в котором показано влияние дыхания на его модель во время видеосъемки. Это простое наглядное сравнение, но оно показывает то, что вы ожидаете: поскольку объективы Tamron и Nikon сфокусированы на МФД, объекты становятся меньше, а на Canon — больше.
Я хотел найти способ количественной оценки этого визуального изменения, и статья Боба Аткинса о сфокусированном дыхании подсказала мне, как это сделать. В качестве объектов он использовал звезды, но я живу в Сиэтле, так что это непрактичный вариант (привет, облачное небо). Поэтому вместо этого я использовал два небольших светодиодных источника света и сделал следующее:
Я сделал недоэкспонированный снимок с диафрагмой f/22 (чтобы уменьшить боке/кружок нерезкости) с датчиком камеры на расстоянии около 26 футов от объектива.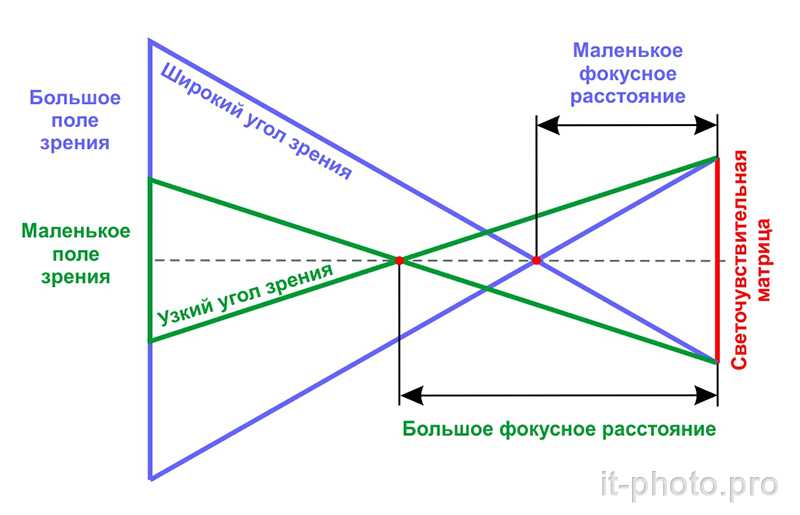 света, с объективом, сфокусированным на этом расстоянии. Объектив, кстати, был Canon 70-200 f/2.8L non-IS, так как я читал, что он ведет себя аналогично IS II, но сам еще не измерял. Выглядело это так:
света, с объективом, сфокусированным на этом расстоянии. Объектив, кстати, был Canon 70-200 f/2.8L non-IS, так как я читал, что он ведет себя аналогично IS II, но сам еще не измерял. Выглядело это так:
Затем я сфокусировал объектив примерно на 12 футов (используя индикатор дальности на объективе), но не двигал камеру . Идея здесь состоит в том, чтобы получить тот же эффект, что и у Мэтта Грейнджера, когда он переключает фокус своего объектива в своем видео, но на некоторых расстояниях, которые я могу измерить.
Затем я сделал снимок с объективом, сфокусированным на 7 футов и 5 футов.
Результаты можно увидеть в этой гифке:
(нажмите, чтобы анимировать)
Как видите, я загрузил эти изображения в Photoshop, установил направляющие, чтобы отметить центры каждого источника света (проще, чем я ожидал, попасть в несколько пикселей от центра), а затем использовал линейку инструмент для измерения расстояния от центра до центра.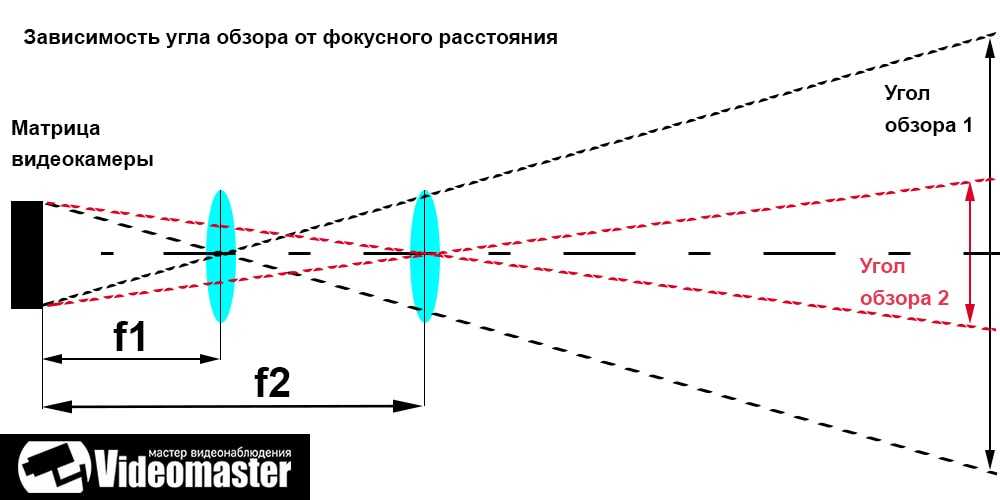 Эти расстояния отмечены на изображениях выше.
Эти расстояния отмечены на изображениях выше.
Но и без цифр видно, что огоньки расходятся; вовлеченные расстояния не особенно тонки. В этом можно убедиться, просто взглянув в объектив и покрутив фокус. (Обратите внимание, что ЦЕНТРЫ источников света расходятся, а не только края. Если бы я просто открыл диафрагму, чтобы увеличить размер размытия, мы бы увидели результаты, имитирующие то, что вы ожидаете от дыхания с нулевым фокусом) .
Но мы можем посмотреть и на числа, вот они в виде таблицы:
| Расстояние (в пикселях) | % от 4041 |
|---|---|
| 4041 | 100% |
| 4230 | 104,68% |
| 4524 | 111,95% |
| 4910 | 121,50% |
После этого я вернулся и измерил фокусное расстояние объектива на каждом из этих расстояний от объекта, используя оригинальный метод, описанный выше. Мои измеренные фокусные расстояния были:
| Измеренное фокусное расстояние @ 26, 12, 7 и 5 футов | % от 199,6 мм |
|---|---|
| 199,6 мм | 100% |
| 206,2 мм | 103,3% |
| 216,0 мм | 108,2% |
| 248,9 мм | 124,7% |
Теперь взгляните на сравнение этих двух наборов чисел.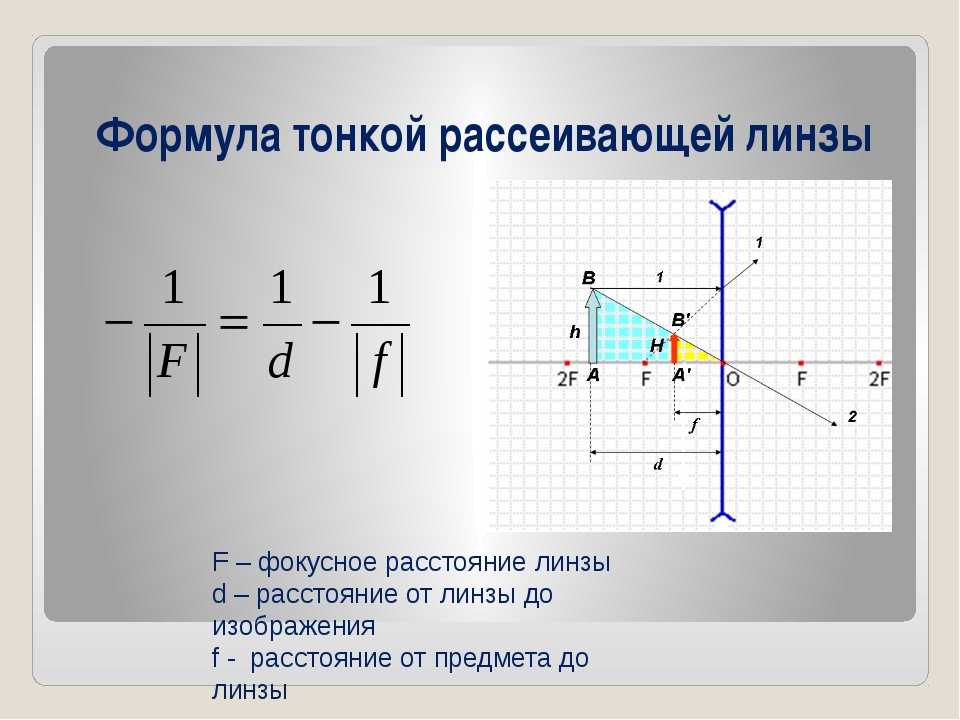
| Расстояние (пиксели) | % от начальной точки | Фокусное расстояние | % от начальной точки |
|---|---|---|---|
| 4041 | 100 % | 199,6 мм | 100 % |
| 4230 | 104,68% | 206,2 мм | 103,3% |
| 4524 | 111,95% | 216,0 мм | 108,2% |
| 4910 | 121,50% | 248,9 мм | 124,7% |
Конечно, они не идеально подходят друг другу, но отчасти причина этого в том, что во втором измерении было много места для небрежности; Мне пришлось установить фокус на 7 футов, глядя на окошко индикатора дальности на объективе, а не фокусируясь, например, на чем-то. Но они все еще довольно близки… худшая разница составляет около 3,75%.
Это означает, что из двух наших разных методов, в одном из которых камера находится в стационарном положении на расстоянии 26 футов от цели, а в другом камера перемещается на расстояние не более 5 футов от цели, числа довольно хорошо поддерживают друг друга.
Некоторые утверждают, что Canon 70-200 f/2.8L и IS II вообще не дышат. Если бы это было так, то оба этих набора измерений должны были бы отличаться не менее чем на 20% на отметке 5 футов, но вряд ли вообще на конце 26 футов!
Есть вопросы? Проблемы?
Я измерил таким образом несколько линз, каждую линзу несколько раз, и все цифры оказались такими, как я и ожидал (после небольшого замешательства в одном случае). Это не моя формула, но уравнение достаточно простое и, безусловно, имеет для меня смысл. Тем не менее, я, безусловно, открыт для возможности того, что есть ошибка или что в нем не хватает чего-то, что сделало бы его более точным. Если это так, и вы можете мне это объяснить, я был бы очень признателен. Пожалуйста, дайте мне знать в комментариях ниже!
С другой стороны, если мне что-то непонятно в отношении какого-либо шага описанной выше процедуры, не стесняйтесь спрашивать. Удачи!
оптика. Определение фокусного расстояния выпуклой линзы
$\begingroup$
Итак, вчера мы сделали практическое задание по физике, где нашли фокусное расстояние выпуклой линзы с помощью эксперимента, в котором у нас было 2 игольчатых объекта и выпуклая линза, помещенная между ними, и нам нужно было отрегулировать линзу в определенным образом. Поскольку изображение объекта (скажем, А) будет перевернутым, его игла будет казаться направленной вниз в линзе, и нам пришлось отрегулировать линзу так, чтобы заостренный конец изображения, которое мы видим с объектом А в линзе, совпадал. incide с заостренным концом объекта B.
Поскольку изображение объекта (скажем, А) будет перевернутым, его игла будет казаться направленной вниз в линзе, и нам пришлось отрегулировать линзу так, чтобы заостренный конец изображения, которое мы видим с объектом А в линзе, совпадал. incide с заостренным концом объекта B.
Но я так и не понял, зачем мы это делаем? Я знаю, что нам нужны две переменные для определения фокусного расстояния: одна (v) расстояние от изображения до линзы, а другая (u) расстояние до объекта от линзы.
У меня много недоразумений по поводу этого эксперимента, поэтому я начну с самого простого.
- Почему мы можем видеть реальное изображение в линзе выпуклой линзы? Почему он кажется внутри выпуклой линзы, я понимаю, почему мы можем видеть мнимое изображение, сформированное вогнутой линзой, как сформированное внутри линзы, поскольку, когда мы прослеживаем световые лучи назад, мы, кажется, получаем изображение позади Объектив.
Но поскольку изображение, формируемое выпуклой линзой, реально и пересекается в точке перед линзой, почему я могу видеть ее перевернутое изображение, формируемое внутри линзы? Разве мне не нужен экран для получения изображения, и если сетчатка моих глаз выступает здесь как экран, то почему я вижу, как он формируется внутри хрусталика?
2) Итак, еще одна загадка, которая мне кажется, заключается в том, почему у нас есть еще одна игла (Объект B), и мы должны поместить ее определенным образом (как описано выше) и то расстояние, которое мы измеряем от Объекта B, когда он помещен таким образом определяется расстояние до изображения, формируемого выпуклой линзой объекта А? Я просто не могу понять, как это будет.
Я надеюсь, что кто-нибудь поймет мой запрос и разрешит его.
- оптика
- видимый свет
- экспериментальная физика
- геометрическая оптика
- линзы
$\endgroup$
1
$\begingroup$
В используемом вами методе необходимо выполнить два измерения, поскольку используется соотношение $\frac{1}{f}=\frac{1}{d_o}+\frac{1}{d_i}$ поэтому вам нужно измерить расстояния до объекта и изображения, $d_o$ и $d_i$. Другой распространенный метод измерения фокусного расстояния состоит в том, чтобы найти расстояние до изображения объекта, который находится достаточно далеко, чтобы расстояние до объекта можно было считать бесконечным. В этом случае $f=d_i$.
Чтобы ответить на вопрос, почему вы можете видеть реальное изображение, полезно вспомнить, что изображения выглядят как объекты, потому что свет исходит от изображений точно так же, как и от объекта. Реальное изображение формируется перед линзой, то есть на той же стороне линзы, что и вы, и противоположной стороне по сравнению с объектом А. Лучи света от предмета проходят через линзу, сходятся в точке изображения, а затем снова расходятся. Вы говорите о том, что видите изображение «в линзе», и это правда, что изображение должно быть расположено между вашим глазом и линзой, но если вы внимательно посмотрите и слегка повернете голову, глядя на изображение, вы обнаружите, что оно ведет себя так, как будто оно находились перед объективом, а не за ним, как в мнимом изображении.
Реальное изображение формируется перед линзой, то есть на той же стороне линзы, что и вы, и противоположной стороне по сравнению с объектом А. Лучи света от предмета проходят через линзу, сходятся в точке изображения, а затем снова расходятся. Вы говорите о том, что видите изображение «в линзе», и это правда, что изображение должно быть расположено между вашим глазом и линзой, но если вы внимательно посмотрите и слегка повернете голову, глядя на изображение, вы обнаружите, что оно ведет себя так, как будто оно находились перед объективом, а не за ним, как в мнимом изображении.
Вы можете держать экран (лист бумаги) в точке, где формируется изображение, и вы сможете увидеть проецируемое на него реальное изображение, хотя, скорее всего, это не так. Это работало бы более надежно, если бы вы использовали свечу или другой светящийся предмет. Что касается сетчатки вашего глаза, то здесь происходит то, что хрусталик вашего глаза (с роговицей) формирует реальное изображение на вашей сетчатке. Этот процесс одинаков независимо от того, смотрите ли вы на реальное изображение, на виртуальное изображение или на сам исходный объект.
Этот процесс одинаков независимо от того, смотрите ли вы на реальное изображение, на виртуальное изображение или на сам исходный объект.
В лабораторной процедуре вы пытаетесь поместить объект B так, чтобы он совпал с изображением объекта A. Идея состоит в том, что если поставить его в нужное место, вы можете немного подвигать головой, и изображение объекта A и объекта B должно казаться, что они остаются вместе. Если вам кажется, что они движутся относительно друг друга, когда вы меняете точку зрения, вы знаете, что они еще не находятся в одном и том же месте.
Это может показаться сложным способом измерения фокусного расстояния, но он дает вам некоторый опыт работы с реальными изображениями.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
. Преломление
Преломлениеи лучевая модель света
Диаграммы лучей можно использовать для определения местоположения, размера, ориентации и типа изображения, образованного объектами, помещенными в заданное место перед линзой. Использование этих диаграмм было продемонстрировано ранее в Уроке 5 как для собирающих, так и для рассеивающих линз. Лучевые диаграммы предоставляют полезную информацию об отношениях объект-изображение, но не могут предоставить информацию в количественной форме. Хотя лучевая диаграмма может помочь определить приблизительное местоположение и размер изображения, она не дает числовой информации о расстоянии до изображения и размере изображения. Чтобы получить этот тип числовой информации, необходимо использовать Уравнение линзы и Уравнение увеличения . Уравнение линзы выражает количественную связь между расстоянием до объекта (d o ), расстоянием до изображения (d i ) и фокусным расстоянием (f).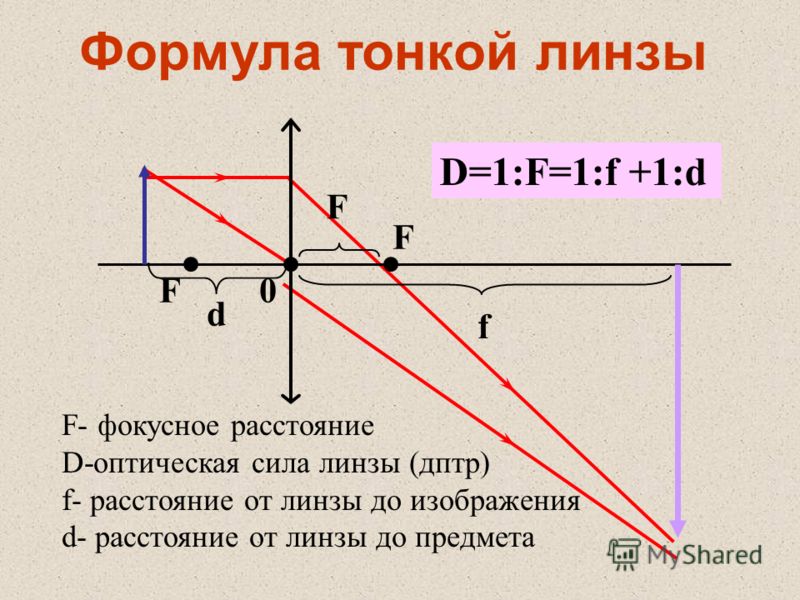 Уравнение формулируется следующим образом:
Уравнение формулируется следующим образом:
Уравнение увеличения связывает отношение расстояния до изображения и расстояния до объекта с отношением высоты изображения (h i ) и высоты объекта (h o ). Уравнение увеличения формулируется следующим образом:
Эти два уравнения можно объединить, чтобы получить информацию о расстоянии до изображения и высоте изображения, если известно расстояние до объекта, высота объекта и фокусное расстояние.
Практические задачиВ качестве демонстрации эффективности уравнения линзы и уравнения увеличения рассмотрим следующую примерную задачу и ее решение.
Лампа высотой 4,00 см расположена на расстоянии 45,7 см от двояковыпуклой линзы с фокусным расстоянием 15,2 см. Определите расстояние до изображения и размер изображения.
Как и все проблемы в физике, начните с идентификации известной информации.
Затем укажите неизвестные величины, для которых вы хотите найти решение.
Для определения расстояния до изображения необходимо использовать уравнение линзы. Следующие строки представляют решение расстояния изображения; показаны замены и алгебраические шаги.
1/(15,2 см) = 1/(45,7 см) + 1/d i
0,0658 см -1 = 0,0219 см -1 + 1/d i
0,0439 см -1 = 1/d i
Численные значения в приведенном выше решении были округлены при записи, однако во всех расчетах использовались неокругленные числа. Окончательный ответ округляется до третьей значащей цифры.
Окончательный ответ округляется до третьей значащей цифры.
Для определения высоты изображения необходимо уравнение увеличения. Поскольку три из четырех величин в уравнении (без учета M) известны, можно вычислить четвертую величину. Решение показано ниже.
ч i /(4,00 см) = — (22,8 см)/(45,7 см)
ч i = — (4,00 см) • (22,8 см)/(45,7 см)
Отрицательные значения высоты изображения указывают на то, что изображение является перевернутым. Как это часто бывает в физике, отрицательный или положительный знак перед числовым значением физической величины представляет информацию о направлении. В случае высоты изображения отрицательное значение всегда указывает на перевернутое изображение.
Из расчетов в этой задаче можно сделать вывод, что если предмет высотой 4,00 см поместить на расстоянии 45,7 см от двояковыпуклой линзы с фокусным расстоянием 15,2 см, то изображение будет перевернутым, 1,99 см высотой и расположен на расстоянии 22,8 см от линзы. Результаты этого расчета согласуются с принципами, обсуждавшимися ранее в этом уроке. В этом случае объект расположен на дальше точки 2F (которая будет на расстоянии двух фокусных расстояний от линзы), а изображение расположено между точкой 2F и фокальной точкой. Это попадает в категорию Случая 1: Объект расположен на за 2F для собирающей линзы.
Теперь давайте попробуем второй пример задачи:
Лампа высотой 4,00 см помещена на расстоянии 8,30 см от двояковыпуклой линзы с фокусным расстоянием 15,2 см. (ПРИМЕЧАНИЕ: это тот же объект и та же линза, только на этот раз объект расположен ближе к линзе.) Определите расстояние до изображения и размер изображения.
Опять же, начнем с идентификации известной информации.
Затем укажите неизвестные величины, для которых вы хотите найти решение.
Для определения расстояния до изображения необходимо использовать уравнение линзы. Следующие строки представляют решение расстояния изображения; показаны замены и алгебраические шаги.
1/(15,2 см) = 1/(8,30 см) + 1/d i
0,0658 см -1 = 0,120 см -1 + 1/d i
-0,0547 см -1 = 1/d i
Численные значения в приведенном выше решении были округлены при записи, однако во всех расчетах использовались неокругленные числа. Окончательный ответ округляется до третьей значащей цифры.
Окончательный ответ округляется до третьей значащей цифры.
Для определения высоты изображения необходимо уравнение увеличения. Поскольку три из четырех величин в уравнении (без учета M) известны, можно вычислить четвертую величину. Решение показано ниже.
ч i /(4,00 см) = — (-18,3 см)/(8,30 см)
ч i = — (4,00 см) • (-18,3 см)/(8,30 см)
Отрицательное значение расстояния до изображения указывает на то, что изображение является виртуальным изображением, расположенным со стороны объектива со стороны объекта. Опять же, отрицательный или положительный знак перед числовым значением физической величины представляет информацию о направлении. В случае расстояния до изображения отрицательное значение всегда означает, что изображение расположено на стороне объекта от линзы. Обратите также внимание, что высота изображения является положительным значением, что означает вертикальное изображение. Любое изображение, которое находится в вертикальном положении и расположено со стороны объекта от линзы, считается виртуальным изображением.
Обратите также внимание, что высота изображения является положительным значением, что означает вертикальное изображение. Любое изображение, которое находится в вертикальном положении и расположено со стороны объекта от линзы, считается виртуальным изображением.
Из расчетов по второму образцу задачи можно сделать вывод, что если предмет высотой 4,00 см поместить на расстоянии 8,30 см от двояковыпуклой линзы с фокусным расстоянием 15,2 см, то изображение будет увеличенным, прямым, 8,81- см высотой и расположен на расстоянии 18,3 см от линзы со стороны предмета. Результаты этого расчета согласуются с принципами, обсуждавшимися ранее в этом уроке. В этом случае объект находится перед фокусом (т. е. расстояние до объекта меньше фокусного расстояния), а изображение — за линзой. Это относится к категории случая 5: объект расположен перед F (для собирающей линзы).
Третья примерная задача относится к рассеивающей линзе.
Лампа высотой 4,00 см расположена на расстоянии 35,5 см от рассеивающей линзы с фокусным расстоянием -12,2 см.Определите расстояние до изображения и размер изображения.
Как и все проблемы в физике, начните с идентификации известной информации.
Затем укажите неизвестные величины, для которых вы хотите найти решение.
Для определения расстояния до изображения необходимо использовать уравнение линзы. Следующие строки представляют решение расстояния изображения; показаны замены и алгебраические шаги.
1/(-12,2 см) = 1/(35,5 см) + 1/d i
-0,0820 см -1 = 0,0282 см -1 + 1/d i
-0,110 см -1 = 1/d i
Численные значения в приведенном выше решении были округлены при записи, однако во всех расчетах использовались неокругленные числа. Окончательный ответ округляется до третьей значащей цифры.
Окончательный ответ округляется до третьей значащей цифры.
Для определения высоты изображения необходимо уравнение увеличения. Поскольку три из четырех величин в уравнении (без учета M) известны, можно вычислить четвертую величину. Решение показано ниже.
ч i /(4,00 см) = — (-9,08 см)/(35,5 см)
ч i = — (4,00 см) * (-9,08 см)/(35,5 см)
Отрицательные значения расстояния до изображения указывают на то, что изображение расположено со стороны объекта от линзы. Как уже упоминалось, отрицательный или положительный знак перед числовым значением физической величины представляет информацию о направлении. В случае расстояния до изображения отрицательное значение всегда указывает на существование мнимого изображения, расположенного со стороны объектива со стороны объекта. В случае высоты изображения положительное значение указывает на вертикальное изображение.
В случае высоты изображения положительное значение указывает на вертикальное изображение.
Из расчетов в этой задаче можно сделать вывод, что если предмет высотой 4,00 см поместить на расстоянии 35,5 см от рассеивающей линзы с фокусным расстоянием 12,2 см, то изображение будет прямым, высотой 1,02 см и расположенным на 9,08 см от линзы со стороны предмета. Результаты этого расчета согласуются с принципами, обсуждавшимися ранее в этом уроке. Рассеивающие линзы всегда дают изображения, которые являются прямыми, виртуальными, уменьшенными в размере и расположенными со стороны предмета линзы.
Практика ведет к совершенству!
Используйте виджет Find the Image Distance ниже, чтобы исследовать влияние фокусного расстояния и расстояния до объекта на расстояние до изображения. Просто введите фокусное расстояние и расстояние до объекта. Затем нажмите кнопку Calculate Image Distance , чтобы просмотреть результат. Используйте виджет как тренировочный инструмент.
Используйте виджет как тренировочный инструмент.
Расследуй!
Постоянная задача фотографов — создать изображение, на котором как можно больше сфокусировано на объекте. Цифровые камеры используют линзы для фокусировки изображения на сенсорной пластине на том же расстоянии от линзы. Тем не менее, в этом уроке мы узнали, что расстояние до изображения зависит от расстояния до объекта. Так как же фотограф может сфокусировать объекты в поле зрения, если они находятся на разном расстоянии от камеры? Это постоянная проблема для фотографов (будь то любители-энтузиасты или профессионалы), которые хотят контролировать, какая часть объекта находится в фокусе. Глубина резкости — это термин фотографа для описания расстояния от ближайшего до самого дальнего объекта в поле зрения, которые приемлемо сфокусированы на фотографии. Виджет Фотография и глубина резкости позволяет исследовать переменные, влияющие на глубину резкости.
f-stop или f-число объектива камеры связано с размером круглого отверстия или апертуры, через которую проходит свет на пути к цифровому датчику. Чем больше число f, тем меньше отверстие и тем меньше света попадает на сенсор. кружок нерезкости связан с ограничением глаза для разрешения деталей изображения в пределах небольшой области. Для 35-мм камеры, изображения которой увеличены до размера отпечатка 5×7 дюймов, общепринятое значение кружка нерезкости составляет 0,0333 мм.
Условные обозначения
Условные обозначения для заданных величин в уравнении линзы и уравнениях увеличения следующие:0028

Подобно многим математическим задачам в физике, этот навык приобретается только благодаря длительной личной практике. Возможно, вы хотели бы потратить некоторое время, чтобы решить следующие задачи.
Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного стенда Optics Bench. Вы можете найти это в разделе Physics Interactives на нашем сайте. Интерактивная скамья Optics Bench предоставляет учащимся интерактивную среду для изучения формирования изображений линзами и зеркалами. Это как полный набор оптических инструментов на вашем экране.
Это как полный набор оптических инструментов на вашем экране.
Посетите: Optics Bench Interactive
1. Определите расстояние до изображения и высоту изображения для объекта высотой 5 см, расположенного на расстоянии 45,0 см от двояковыпуклой линзы с фокусным расстоянием 15,0 см.
2. Определите расстояние до изображения и высоту изображения для объекта высотой 5 см, расположенного на расстоянии 30,0 см от двояковыпуклой линзы с фокусным расстоянием 15,0 см.
3. Определить расстояние до изображения и высоту изображения для объекта высотой 5 см, расположенного на расстоянии 20,0 см от двояковыпуклой линзы с фокусным расстоянием 15,0 см.
4. Определить расстояние до изображения и высоту изображения для объекта высотой 5 см, расположенного на расстоянии 10,0 см от двояковыпуклой линзы с фокусным расстоянием 15,0 см.
5. Увеличенное перевернутое изображение расположено на расстоянии 32,0 см от двояковыпуклой линзы с фокусным расстоянием 12,0 см. Определите расстояние до объекта и скажите, является ли изображение реальным или виртуальным.
6. ZINGER : Перевернутое изображение увеличивается в 2 раза, когда объект находится на расстоянии 22 см от двояковыпуклой линзы. Определить расстояние до изображения и фокусное расстояние линзы.
7. Двойная вогнутая линза имеет фокусное расстояние -10,8 см. Предмет находится на расстоянии 32,7 см от поверхности линзы. Определить расстояние до изображения.
8. Определите фокусное расстояние двояковыпуклой линзы, дающей изображение на расстоянии 16,0 см за линзой, когда предмет находится на расстоянии 28,5 см от линзы.
9. Монета диаметром 2,8 см находится на расстоянии 25,0 см от двояковыпуклой линзы с фокусным расстоянием -12,0 см. Определите расстояние изображения и диаметр изображения.
Монета диаметром 2,8 см находится на расстоянии 25,0 см от двояковыпуклой линзы с фокусным расстоянием -12,0 см. Определите расстояние изображения и диаметр изображения.
10. Фокус расположен на расстоянии 20,0 см от двояковыпуклой линзы. Предмет находится на расстоянии 12 см от линзы. Определить расстояние до изображения.
Перейти к следующему уроку:
Фокусное расстояние и поле зрения
Объективы с фиксированным фокусным расстоянием
Объективы с фиксированным фокусным расстоянием, также известные как обычные или энтоцентрические линзы, представляют собой линзы с фиксированным угловым полем зрения (AFOV). Фокусируя объектив на разные рабочие расстояния, можно получить поля зрения (FOV) разного размера, хотя угол обзора остается постоянным. AFOV обычно указывается как полный угол (в градусах), связанный с горизонтальным размером (шириной) сенсора, с которым будет использоваться объектив.
Примечание: Объективы с фиксированным фокусным расстоянием не следует путать с объективами с фиксированным фокусным расстоянием. Объективы с фиксированным фокусным расстоянием могут фокусироваться на разных расстояниях; Объективы с фиксированным фокусом предназначены для использования на одном определенном рабочем расстоянии. Примерами линз с фиксированным фокусом являются многие телецентрические линзы и объективы для микроскопов.
Фокусное расстояние объектива определяет угловое поле зрения объектива. Для данного размера сенсора, чем короче фокусное расстояние, тем шире угловое поле объектива. Кроме того, чем короче фокусное расстояние объектива, тем меньше расстояние, необходимое для получения того же FOV по сравнению с объективом с большим фокусным расстоянием. Для простой тонкой выпуклой линзы фокусное расстояние — это расстояние от задней части линзы до плоскости изображения, образованного объектом, расположенным бесконечно далеко перед линзой. Из этого определения можно показать, что угловое поле зрения объектива связано с фокусным расстоянием (уравнение 1), где f — фокусное расстояние в миллиметрах, а h — горизонтальный размер датчика в миллиметрах (рис. 1). ).
1). ).
Рис. 1. Для заданного размера сенсора h более короткое фокусное расстояние дает более широкое поле зрения
В целом, однако, фокусное расстояние измеряется от задней главной плоскости объектива, которая редко располагается на механической задней части объектива. визуализирующий объектив; это одна из причин того, что рабочие расстояния, рассчитанные с использованием параксиальных уравнений, являются лишь приблизительными значениями, а механическая конструкция системы должна быть разработана только с использованием данных, полученных с помощью компьютерного моделирования, или данных, взятых из таблиц спецификаций объективов. Параксиальные расчеты, как с помощью калькуляторов линз, являются хорошей отправной точкой для ускорения процесса выбора линз, но полученные числовые значения следует использовать с осторожностью.
При использовании объективов с фиксированным фокусным расстоянием существует три способа изменить поле зрения системы (камеры и объектива). Первый и часто самый простой вариант — изменить рабочее расстояние от объектива до объекта; перемещение объектива дальше от плоскости объекта увеличивает поле зрения. Второй вариант — заменить используемый объектив на другой с другим фокусным расстоянием. Третий вариант — изменить размер используемого сенсора; датчик большего размера обеспечит большее поле зрения при том же рабочем расстоянии, как определено в уравнении 1.
Первый и часто самый простой вариант — изменить рабочее расстояние от объектива до объекта; перемещение объектива дальше от плоскости объекта увеличивает поле зрения. Второй вариант — заменить используемый объектив на другой с другим фокусным расстоянием. Третий вариант — изменить размер используемого сенсора; датчик большего размера обеспечит большее поле зрения при том же рабочем расстоянии, как определено в уравнении 1.
Хотя часто бывает удобно иметь очень широкое угловое поле зрения, следует учитывать некоторые недостатки. Во-первых, уровень искажения, который связан с некоторыми объективами с коротким фокусным расстоянием, может сильно влиять на фактическую AFOV и может вызывать изменения угла по отношению к рабочему расстоянию (WD) из-за различной величины искажения. Далее, объективы с коротким фокусным расстоянием, как правило, с трудом достигают наивысшего уровня производительности по сравнению с объективами с большим фокусным расстоянием (см. Рекомендацию № 3). Кроме того, у объективов с коротким фокусным расстоянием могут возникнуть трудности с охватом сенсоров среднего и большого размера, что может ограничить их удобство использования, как обсуждалось в разделе «Относительная освещенность сенсора, закругление и виньетирование».
Другой способ изменить поле зрения системы — использовать вариообъектив или зум-объектив; эти типы линз позволяют регулировать их фокусное расстояние и, таким образом, имеют переменные угловые поля зрения. Варифокальные и зум-объективы часто имеют недостатки с точки зрения размера и стоимости по сравнению с объективами с фиксированным фокусным расстоянием и часто не могут обеспечить такой же уровень производительности, как объективы с фиксированным фокусным расстоянием.
Использование WD и FOV для определения фокусного расстояния
Во многих приложениях требуемое расстояние до объекта и желаемое поле зрения (обычно размер объекта с дополнительным буферным пространством) являются известными величинами. Эту информацию можно использовать для непосредственного определения требуемого углового поля зрения с помощью формул, показанных в уравнении 2, где WD — рабочее расстояние от объектива, а AFOV — угловое поле зрения. Уравнение 2 эквивалентно нахождению угла при вершине треугольника, высота которого равна рабочему расстоянию, а основание равно горизонтальному полю зрения, как показано на рисунке 2. 9.0802 Примечание: На практике вершина этого треугольника редко находится на механической передней части линзы, от которой измеряется рабочее расстояние, и ее следует использовать только в качестве приблизительного значения, если не известно расположение входного зрачка.
9.0802 Примечание: На практике вершина этого треугольника редко находится на механической передней части линзы, от которой измеряется рабочее расстояние, и ее следует использовать только в качестве приблизительного значения, если не известно расположение входного зрачка.
Рис. 2. Соотношение между HFOV, размером сенсора и WD для заданного углового поля зрения
После определения требуемого AFOV фокусное расстояние можно приблизительно определить с помощью уравнения 1, а подходящий объектив можно выбрать из спецификации объектива. таблицу или техническое описание, найдя ближайшее доступное фокусное расстояние с необходимым угловым полем зрения для используемого сенсора.
Значение 14,25°, полученное в примере 1, можно использовать для определения необходимой линзы, но необходимо также выбрать размер сенсора. По мере увеличения или уменьшения размера сенсора будет изменяться объем используемого изображения объектива; это изменит AFOV системы и, следовательно, общий FOV. Чем больше сенсор, тем больше можно получить угол обзора при том же фокусном расстоянии. Например, объектив 25 мм можно использовать с датчиком ½ дюйма (6,4 мм по горизонтали), а объектив 35 мм можно использовать с датчиком 2/3 дюйма (8,8 мм по горизонтали), поскольку оба они будут обеспечивать угол обзора примерно 14,5° на соответствующие датчики.
Чем больше сенсор, тем больше можно получить угол обзора при том же фокусном расстоянии. Например, объектив 25 мм можно использовать с датчиком ½ дюйма (6,4 мм по горизонтали), а объектив 35 мм можно использовать с датчиком 2/3 дюйма (8,8 мм по горизонтали), поскольку оба они будут обеспечивать угол обзора примерно 14,5° на соответствующие датчики.
В качестве альтернативы, если датчик уже выбран, фокусное расстояние можно определить непосредственно из FOV и WD, подставив уравнение 1 в уравнение 2, как показано в уравнении 3, где h — размер датчика по горизонтали (количество пикселей по горизонтали). умножается на размер пикселя), а f — фокусное расстояние объектива в миллиметрах; FOV и WD должны измеряться в одной и той же системе единиц. Как указывалось ранее, следует учитывать некоторую степень гибкости рабочего расстояния системы, поскольку приведенные выше примеры являются лишь приблизительными значениями первого порядка, а также не учитывают искажения.
Расчет поля зрения с использованием объектива с фиксированным увеличением
Как правило, объективы с фиксированным увеличением имеют фиксированный или ограниченный диапазон рабочих расстояний. Хотя использование телецентрического или другого объектива с фиксированным увеличением может быть более ограниченным, поскольку они не позволяют использовать разные поля зрения при изменении рабочего расстояния, расчеты для них очень просты, как показано в уравнении 4.
Хотя использование телецентрического или другого объектива с фиксированным увеличением может быть более ограниченным, поскольку они не позволяют использовать разные поля зрения при изменении рабочего расстояния, расчеты для них очень просты, как показано в уравнении 4.
Поскольку желаемое поле зрения и датчик часто известны, процесс выбора объектива можно упростить, преобразовав уравнение 4 в уравнение 5.
Если требуемое увеличение уже известно, а рабочее расстояние ограничено, уравнение 3 можно изменить (заменив h/FOV на увеличение) и использовать для определения подходящего объектива с фиксированным фокусным расстоянием, как показано в уравнении 6.
Имейте в виду что уравнение 6 является приблизительным и быстро ухудшается при увеличении более 0,1 или при коротких рабочих расстояниях. Для увеличения более 0,1 следует использовать объектив с фиксированным увеличением или компьютерное моделирование (например, Zemax) с соответствующей моделью объектива. По тем же причинам калькуляторы объективов, которые обычно можно найти в Интернете, следует использовать только для справки. Если вы сомневаетесь, сверьтесь с таблицей характеристик объектива.
Если вы сомневаетесь, сверьтесь с таблицей характеристик объектива.
Примечание: Горизонтальное поле зрения обычно используется при обсуждении поля зрения из соображений удобства, но необходимо учитывать соотношение сторон сенсора (отношение ширины сенсора к его высоте), чтобы гарантировать, что весь объект помещается в поле зрения. изображение (уравнение 7), где соотношение сторон используется в виде дроби (например, 4:3 = 4/3). В то время как большинство датчиков 4:3, 5:4 и 1:1 также довольно распространены. Это различие в соотношении сторон также приводит к различным размерам датчиков одного и того же формата. Все уравнения, используемые в этом разделе, также могут быть использованы для вертикального FOV, если вертикальный размер сенсора заменяется горизонтальным размером, указанным в уравнениях.
ПРИМЕРЫ ФОКУСНОГО РАССТОЯНИЯ ОБЪЕКТИВА
Использование WD и FOV для определения фокусного расстояния
Пример 1: Для системы с желаемым рабочим расстоянием 200 мм и горизонтальным полем зрения 50 мм, каково угловое поле зрения ( АФОВ)?
Расчет FOV с использованием объектива с фиксированным увеличением
Пример 2: Для приложения, использующего ½-дюймовый сенсор с размером сенсора по горизонтали 6,4 мм, желательно горизонтальное FOV 25 мм.
Просмотрев список объективов с фиксированным или телецентрическим увеличением, можно выбрать нужное увеличение. Примечание. По мере увеличения увеличения размер поля зрения будет уменьшаться; обычно желательно увеличение меньше расчетного, чтобы можно было визуализировать все поле зрения. В случае Примера 2 наиболее распространенным вариантом является объектив с увеличением 0,25X, который дает поле зрения 25,6 мм на том же датчике.
Light Vortex Astronomy — Статья: Как очень точно рассчитать эффективное фокусное расстояние вашего телескопа
Статья (захват изображения):
Как очень точно рассчитать эффективное фокусное расстояние вашего телескопа
Возможно, вы читаете это, думая, что в этом нет абсолютно никакого смысла, поскольку если ваш производитель сообщает вам фокусное расстояние вашего телескопа, а вы используете Известный экстендер/редуктор фокусного расстояния позволяет легко определить эффективное фокусное расстояние. Почему это вообще важно? Что ж, некоторым из нас нравится изображать мозаику. Когда дело доходит до изображения мозаики, нужно хорошо знать эффективное фокусное расстояние телескопа и камеры, чтобы правильно рассчитать поле зрения, что, в свою очередь, приводит к хорошо перекрывающимся сегментам мозаичного изображения. Я хотел бы начать с извинений, потому что я не могу просто привести математическое уравнение без его вывода. Я ненавижу, когда мне дают уравнения, а не то, как они к ним приходят. Итак, вот краткий вывод уравнения, которое даст вам эффективное фокусное расстояние вашего телескопа при попытке Диаграммы Microsoft Paint , чтобы сопровождать математику. Выше приведена очень, очень упрощенная схема установки телескоп-камера. Луч света входит в OTA и фокусируется на ПЗС-датчике ПЗС-камеры. ПЗС-датчик состоит из ячеек — физических ячеек , куда попадают фотоны света. Естественно, эти ячейки имеют конечный размер. Таким образом, размер пикселя в ваших изображениях частично определяется этим физическим размером ячейки вашего ПЗС-сенсора и образует следующий треугольник с фокусным расстоянием. Выше я называю FL фокусным расстоянием телескопа, PS размером пикселя и θ , следовательно, углом. Как вы можете себе представить, моя диаграмма треугольника сильно преувеличена в масштабе. Пиксель намного, намного меньше, чем показано на моей диаграмме. Следовательно, угол θ на самом деле крошечный. В тригонометрическом приближении tan θ ≈ θ , поэтому мы можем фактически написать выше: Угол.  Однако иногда это не так просто. Например, Skywatcher производит свой 2-дюймовый корректор комы для f/4-f/6 9.0007 (оптимизированы для их диапазона f/5 ) и ничего не говорят об изменении эффективного фокусного расстояния. Однако быстрый тест и расчеты показывают, что на самом деле это также и фокальный редуктор 0,9x . Доказательство этому позже. Кроме того, мой телескоп Altair Astro 8″ RC соединен с моим телекомпрессором Astro-Physics CCDT67 , и это дает эффект уменьшения фокуса в зависимости от расстояния вашего датчика CCD от объектива телекомпрессора. Вы можете предсказать это, если знаете расстояние очень точно, но я чувствую, что лучше знать эффективное фокусное расстояние прямо из вещественных доказательств.0003
Однако иногда это не так просто. Например, Skywatcher производит свой 2-дюймовый корректор комы для f/4-f/6 9.0007 (оптимизированы для их диапазона f/5 ) и ничего не говорят об изменении эффективного фокусного расстояния. Однако быстрый тест и расчеты показывают, что на самом деле это также и фокальный редуктор 0,9x . Доказательство этому позже. Кроме того, мой телескоп Altair Astro 8″ RC соединен с моим телекомпрессором Astro-Physics CCDT67 , и это дает эффект уменьшения фокуса в зависимости от расстояния вашего датчика CCD от объектива телекомпрессора. Вы можете предсказать это, если знаете расстояние очень точно, но я чувствую, что лучше знать эффективное фокусное расстояние прямо из вещественных доказательств.0003
 Простая тригонометрия дает следующее соотношение:
Простая тригонометрия дает следующее соотношение: tan θ = PS / FL
θ = PS / FL
θ = PS / FL [радиан на пиксель]
т. е. единица θ на самом деле составляет радиан на пиксель . Однако в астрофотографии нам гораздо больше знакома единица угловых секунд на пиксель , которая является мерой достигнутого или достижимого разрешения. В круге 2π радиан , что равно 360° . Это означает, что 360/2π = 57,29.578° на радиан . В каждом градусе содержится 60 угловых минут , а в каждом угловых минутах содержится 60 угловых секунд . Это означает, что на каждые градусов фактически приходится 60 x 60 = 3600 угловых секунд . Итак, сколько угловых секунд содержится в радианах ? Простой, то есть 57,29578 x 3600 = 206264,8 угловых секунд на радиан. Это важный результат, потому что теперь мы можем сказать, что:
е. единица θ на самом деле составляет радиан на пиксель . Однако в астрофотографии нам гораздо больше знакома единица угловых секунд на пиксель , которая является мерой достигнутого или достижимого разрешения. В круге 2π радиан , что равно 360° . Это означает, что 360/2π = 57,29.578° на радиан . В каждом градусе содержится 60 угловых минут , а в каждом угловых минутах содержится 60 угловых секунд . Это означает, что на каждые градусов фактически приходится 60 x 60 = 3600 угловых секунд . Итак, сколько угловых секунд содержится в радианах ? Простой, то есть 57,29578 x 3600 = 206264,8 угловых секунд на радиан. Это важный результат, потому что теперь мы можем сказать, что:
θ = (206264,8 x PS ) / FL [угловые секунды на пиксель]
Мы умножили все уравнение (фактически числитель этой дроби) на коэффициент преобразования 206960 7 0 0 6 900 9000 в радианы в порядке от до угловых секунд . Мы также отмечаем, что размер пикселя обычно указывается в микрометров на пиксель , а фокусное расстояние обычно указывается в миллиметрах . Здесь есть разница между величинами расстояния 1000 . Мы можем усвоить это 1000 Разница в приведенном выше уравнении путем деления нашего фактора 206264,8 на 1000 :
Мы также отмечаем, что размер пикселя обычно указывается в микрометров на пиксель , а фокусное расстояние обычно указывается в миллиметрах . Здесь есть разница между величинами расстояния 1000 . Мы можем усвоить это 1000 Разница в приведенном выше уравнении путем деления нашего фактора 206264,8 на 1000 :
θ = (206,2648 x ps) / FL [дуговые кабинеты на Pixel]
8 PS и 8 и 8 и 8 и 8 и 8 и 8 и 8 и 8 и 8 и 8 и 8 и 8 и 8 и 8 и 8 и 8 и 8 и 8 и 8 и [дуги . FL теперь представлены в знакомых единицах: PS соответствует микрометрам на пиксель и FL соответствует миллиметрам . В более привычных терминах мы можем заключить этот вывод с помощью следующего уравнения:
[угловые секунды на пиксель] = (206,2648 x [Размер пикселя в мкм]) / [Фокусное расстояние в мм]
Итак, где это уравнение играет роль? Что ж, мы можем использовать улики, чтобы рассчитать эффективное фокусное расстояние вашего телескопа. Настройте свой телескоп и камеру так, как вы будете использовать их для съемки (с любыми фокусными редукторами/телекомпрессорами, распорками и т. д.), и сделайте один снимок любой цели в ночном небе, которая вам нравится. Убедитесь, что фокусировка хорошая и что вы снимаете достойную экспозицию с многочисленными звездами в поле зрения. На данный момент не используйте биннинг (оставьте значение 9).0006 1×1 ). Получив изображение, загрузите его на Astrometry.net . Это разрешит изображение, т. е. определит, на какую цель вы смотрели, а также пометит все распознаваемые объекты на всем изображении. Здесь важно то, что в соответствии с показанной информацией Калибровка она даст вам очень точное значение шкалы пикселей в угловых секундах на пиксель . Обратите внимание: если вы загружаете изображение, которое было помещено в корзину, скажем 9 0006 2×2 , угловых секунд на пиксель будет вдвое больше .
Настройте свой телескоп и камеру так, как вы будете использовать их для съемки (с любыми фокусными редукторами/телекомпрессорами, распорками и т. д.), и сделайте один снимок любой цели в ночном небе, которая вам нравится. Убедитесь, что фокусировка хорошая и что вы снимаете достойную экспозицию с многочисленными звездами в поле зрения. На данный момент не используйте биннинг (оставьте значение 9).0006 1×1 ). Получив изображение, загрузите его на Astrometry.net . Это разрешит изображение, т. е. определит, на какую цель вы смотрели, а также пометит все распознаваемые объекты на всем изображении. Здесь важно то, что в соответствии с показанной информацией Калибровка она даст вам очень точное значение шкалы пикселей в угловых секундах на пиксель . Обратите внимание: если вы загружаете изображение, которое было помещено в корзину, скажем 9 0006 2×2 , угловых секунд на пиксель будет вдвое больше .
Вооружившись результирующим значением угловых секунд на пиксель вашего изображения , мы можем изменить приведенное выше окончательное уравнение следующим образом:
[Фокусное расстояние в мм] = (206,2648 x [Размер пикселя в мкм]) / [Угловые секунды на пиксель]
С его помощью вы получите очень точное значение эффективного фокусного расстояния вашего телескопа. Еще раз обратите внимание, что если вы загружаете объединенное изображение, вам нужно будет разделить ваши угловых секунд на пиксель 9.0007 сначала на величину биннинга (например, если вы бинировали по 2×2 , разделите значение угловых секунд на пиксель на 2 , прежде чем продолжить). С этого момента, вооружившись этой информацией, а также сведениями о вашем ПЗС-сенсоре (от производителя ПЗС-камеры), вы можете легко рассчитать свое поле зрения в таких источниках, как Sky at Night Field of View Calculator или таких программах, как CCDCalc . . Что очень важно, это даст вам возможность точно определить ваше поле зрения для мозаичного изображения. Кроме того, поскольку апертура вашего телескопа, очевидно, не изменяется, разделив эффективное фокусное расстояние на апертуру, вы можете очень точно рассчитать эффективное фокусное расстояние.
Еще раз обратите внимание, что если вы загружаете объединенное изображение, вам нужно будет разделить ваши угловых секунд на пиксель 9.0007 сначала на величину биннинга (например, если вы бинировали по 2×2 , разделите значение угловых секунд на пиксель на 2 , прежде чем продолжить). С этого момента, вооружившись этой информацией, а также сведениями о вашем ПЗС-сенсоре (от производителя ПЗС-камеры), вы можете легко рассчитать свое поле зрения в таких источниках, как Sky at Night Field of View Calculator или таких программах, как CCDCalc . . Что очень важно, это даст вам возможность точно определить ваше поле зрения для мозаичного изображения. Кроме того, поскольку апертура вашего телескопа, очевидно, не изменяется, разделив эффективное фокусное расстояние на апертуру, вы можете очень точно рассчитать эффективное фокусное расстояние.
Вот пример. Раньше я использовал телескоп Skywatcher Explorer 150PDS с ПЗС-камерой ATIK 383L+ . Я загрузил 7 -минутное воздействие в Luminance (наряду с Skywatcher 2 «Corrector и Hutech IDAS LPS 2″ Фильтр Trunk Trunk Nebula до Astrometry.net . Мне дали разрешение 1,63 угловых секунды на пиксель . Согласно ATIK , размер моей ПЗС-камеры составляет 9 пикселей.0006 5,4 мкм на пиксель , поэтому:
Я загрузил 7 -минутное воздействие в Luminance (наряду с Skywatcher 2 «Corrector и Hutech IDAS LPS 2″ Фильтр Trunk Trunk Nebula до Astrometry.net . Мне дали разрешение 1,63 угловых секунды на пиксель . Согласно ATIK , размер моей ПЗС-камеры составляет 9 пикселей.0006 5,4 мкм на пиксель , поэтому:
[Фокусное расстояние в мм] = (206,2648 x 5,4) / 1,63 = 683,331
С моей оптической системой визуализации эффективное фокусное расстояние телескопа составило 683,331 мм2. Если вы посмотрите на характеристики телескопа производителя, то его фокусное расстояние должно быть
750 мм . Фокусное расстояние 750 мм вместе с диафрагмой 150 мм дает коэффициент фокусного расстояния f/5 , но с фокусным расстоянием 683,331 мм , коэффициент фокусного расстояния на самом деле f/4,556 , а коэффициент уменьшения фокусного расстояния 0,911 x . В сущности, несмотря на то, что Skywatcher не рекламирует свой 2″ Coma Corrector как изменяющий что-либо, он действительно обеспечивает некоторое уменьшение фокуса, что подтверждается. – лично я считаю, что в результате использования этой системы я получил более быструю оптическую систему, а плоскостность изображений была фантастической, – но это должно дать вам представление о важности расчета эффективного фокусного расстояния с вашим изображением. оптический поезд. Оценки может быть достаточно для одиночных изображений, но для мозаик лучше заранее точно знать, с чем вы работаете.
В сущности, несмотря на то, что Skywatcher не рекламирует свой 2″ Coma Corrector как изменяющий что-либо, он действительно обеспечивает некоторое уменьшение фокуса, что подтверждается. – лично я считаю, что в результате использования этой системы я получил более быструю оптическую систему, а плоскостность изображений была фантастической, – но это должно дать вам представление о важности расчета эффективного фокусного расстояния с вашим изображением. оптический поезд. Оценки может быть достаточно для одиночных изображений, но для мозаик лучше заранее точно знать, с чем вы работаете.
Определение фокусного расстояния вогнутой линзы с помощью выпуклой линзы
Фокусное расстояние выпуклой линзы — это расстояние между центром линзы и ее фокусом. Фокусное расстояние оптического инструмента/объекта является мерой того, насколько сильно/резко система сводит/рассекает свет, и является обратной величиной оптической силы системы.
Формула фокусного расстояния выпуклой линзы представляет собой расстояние до объекта, умноженное на расстояние до изображения, деленное на разницу расстояния до объекта и расстояния до изображения.
Здесь мы обсудим, как найти фокусное расстояние выпуклой линзы, проведем эксперимент с выпуклой линзой Класс 12, чтобы получить фокусное расстояние выпуклой линзы.
Чтобы найти фокусное расстояние вогнутой линзы с помощью выпуклой линзы
Теперь мы поймем процедуру определения фокусного расстояния вогнутой линзы с помощью выпуклой линзы:
Цель:
Чтобы определить или Найти фокусное расстояние вогнутой линзы с помощью выпуклой линзы двумя следующими способами:
Линза контактного метода и
Линза бесконтактного метода.
Теоретическая часть:
Вогнутая линза в центре тоньше, чем по краям, по сравнению с выпуклой линзой. Итак, когда белый свет проходит через вогнутую линзу, он распространяется во всех направлениях, и именно поэтому мы называем вогнутую линзу рассеивающей линзой.
Итак, когда белый свет проходит через вогнутую линзу, он распространяется во всех направлениях, и именно поэтому мы называем вогнутую линзу рассеивающей линзой.
Характер формирования изображения в вогнутой линзе виртуальный и уменьшенный.
Теперь мы знаем, что формирование изображения уменьшается, поэтому становится трудно найти его фокусное расстояние. Вот почему мы проводим эксперимент, чтобы найти фокусное расстояние вогнутой линзы с помощью выпуклой линзы. Также существует два метода определения фокусного расстояния вогнутой линзы:
Метод контактной линзы
объектив с фокусным расстоянием fa, то фокусное расстояние F комбинации равно:
1/F = 1/fa + 1/fa
Следовательно, формула для фокусного расстояния вогнутой линзы:
fa = (F X fa)/ (fa — F) см
(Изображение будет загружено в ближайшее время )
Метод бесконтактной линзы
Необходимые материалы:
Теоретическая часть
Реальное изображение (i1), сформированное выпуклой линзой, работает как виртуальный объект для вогнутой линзы. Когда вогнутая линза помещается/прикрепляется между выпуклой линзой и реальным изображением i1, формируется новое реальное изображение, которое называется «i2».0003
Когда вогнутая линза помещается/прикрепляется между выпуклой линзой и реальным изображением i1, формируется новое реальное изображение, которое называется «i2».0003
(Изображение будет загружено в ближайшее время)
Если ‘u’ — расстояние вогнутой линзы от реального изображения i1, а v — расстояние от реального изображения i2, то фокусное расстояние вогнутой линзы равно:
1/f = 1/v — 1/u (Мы называем это формулой фокусного расстояния выпуклой линзы)
И,
f = (uv)/(u-v)
Это формула для фокусного расстояния вогнутой линзы Объектив, в котором говорится, что фокусное расстояние является произведением расстояния до изображения и расстояния до объекта, деленным на разницу между объектом и расстоянием до изображения.
Эксперимент с выпуклой линзой, класс 12
Держите заданную вогнутую линзу с фокусным расстоянием в контакте с выпуклой линзой с фокусным расстоянием f.
 Это образует комбинацию двух контактирующих тонких линз.
Это образует комбинацию двух контактирующих тонких линз.Убедитесь, что линзы расположены между блестящей проволокой и экраном на фиксированном расстоянии от сетки, равном u см.
Экран отрегулирован таким образом, чтобы получить на нем четкое изображение калибра проволоки.
Измерьте расстояние от комбинации линз, соприкасающихся с экраном, которое равно «v» расстоянию.
Теперь, чтобы получить фокусное расстояние комбинированной линзы, имеем следующее:
F = (uv)/(u + v) см фокусное расстояние выпуклой линзы/найти фокусное расстояние выпуклой линзы.
Продолжайте повторять вышеописанный эксперимент, размещая комбинацию тонких линз на разных расстояниях от блестящей проволоки.

Теперь мы рассчитаем среднее значение F, как мы уже делали во многих экспериментах с выпуклыми линзами класса 12.
Используя значение фокусного расстояния вогнутой линзы fa и фокусное расстояние комбинации, то есть F, мы можем получить формулу для фокусного расстояния вогнутой линзы, а затем найти фокусное расстояние вогнутой линзы:
fa = (F X fb)/(fb — F) см
Теперь давайте запишите наши наблюдения для дальнейшего использования:
С.№. | Расстояние между комбинацией линз | Фокусное расстояние | |
| | Объект ‘U’ CM | 13999999139Object ‘U’ CM 9000 | 149. |
1. | | | |
| | | | |
3. | | | |
4. | | | |
5 . Чтобы получить фокусное расстояние выпуклой линзы fb, мы получаем значения …..см. Теперь мы получаем фокусное расстояние данной вогнутой линзы как; fa = (F X fb)/ (fb — F) см = …….см. Зачем изучать эту тему? Эта тема является важным экспериментом, который задается на практическом экзамене. | |||


 3.6А).
3.6А). Они пересекутся в точке S1.
Они пересекутся в точке S1. Это расстояние является фокусом собирающей линзы Сделать это 5 раз. Результаты занести в таблицу 3.1.
Это расстояние является фокусом собирающей линзы Сделать это 5 раз. Результаты занести в таблицу 3.1.
 В качестве величины а2используется расстояние от оптического центра рассеивающей линзы, фокусное расстояние которой надо определить ( в нашем случае это линза 2), до заднего фокусавспомогательной линзы. Величина
В качестве величины а2используется расстояние от оптического центра рассеивающей линзы, фокусное расстояние которой надо определить ( в нашем случае это линза 2), до заднего фокусавспомогательной линзы. Величина 
 Пункты 3.4.5 проделать 5 раз. Результаты измерений и вычислений занести в таблицу 3.2.
Пункты 3.4.5 проделать 5 раз. Результаты измерений и вычислений занести в таблицу 3.2.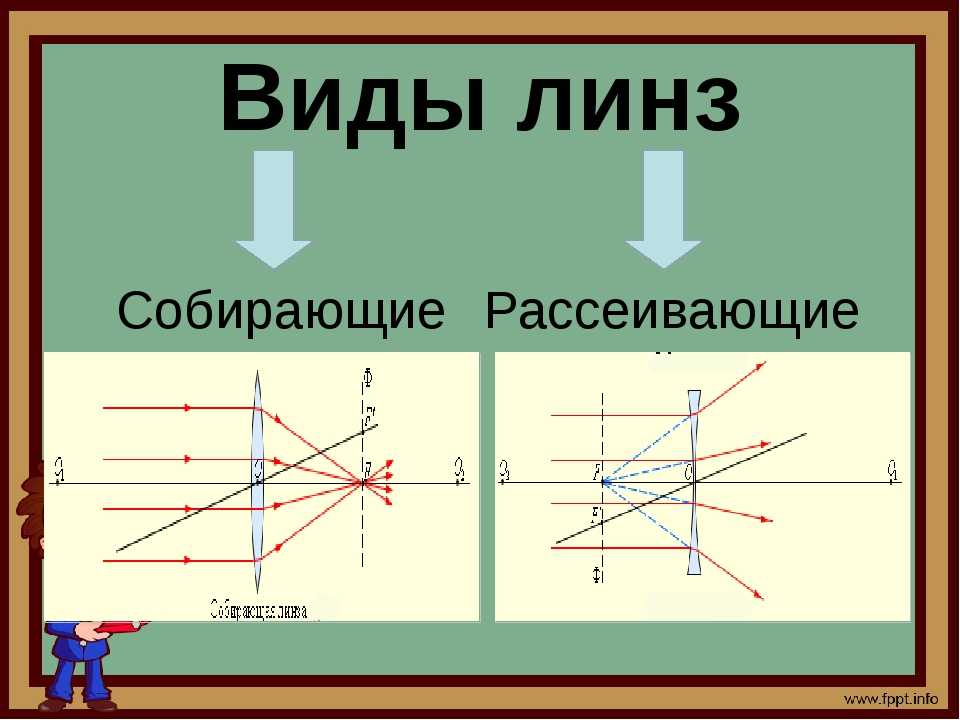 Определить длину волны света, излучаемую лазером
Определить длину волны света, излучаемую лазером п
п
 Измерить расстояние l2. и ∆L Считая угол расхождения лучей ψ малым, рассчитать его величину
Измерить расстояние l2. и ∆L Считая угол расхождения лучей ψ малым, рассчитать его величину Измерить расстояние a между линзой и экраном. Измерить расстояние между соседними интерференционны-ми полосами. Для этого сосчи-тать число полос n, приходящихся на некоторую длину l миллиметровой бумаги (1–2см). Тогда ΔХ= l/(n−1). Результаты занести в таблицу 6.2.
Измерить расстояние a между линзой и экраном. Измерить расстояние между соседними интерференционны-ми полосами. Для этого сосчи-тать число полос n, приходящихся на некоторую длину l миллиметровой бумаги (1–2см). Тогда ΔХ= l/(n−1). Результаты занести в таблицу 6.2.
 Включить лазер в сеть.
Включить лазер в сеть.
 95 Записать полученный результат в виде l=<l>±Δl
95 Записать полученный результат в виде l=<l>±Δl n0 = A / h. (11.2)
n0 = A / h. (11.2) На рис.11.3 показана вольт-амперная характеристика вакуумного фотоэлемента. Для её объяснения надо учесть следующие обстоятельства.
На рис.11.3 показана вольт-амперная характеристика вакуумного фотоэлемента. Для её объяснения надо учесть следующие обстоятельства. Величина задерживающей разности потенциалов зависит от максимальной энергии электронов (11.3), вылетевших с поверхности катода, а также от геометрии электродов.
Величина задерживающей разности потенциалов зависит от максимальной энергии электронов (11.3), вылетевших с поверхности катода, а также от геометрии электродов. .
.
 3. Снять люкс-амперную характеристику.
3. Снять люкс-амперную характеристику. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.039 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.039 с.) 3) связаны с фокусным расстоянием формулой линзы:
3) связаны с фокусным расстоянием формулой линзы: Запишем формулы тонкой линзы для обоих положений:
Запишем формулы тонкой линзы для обоих положений:


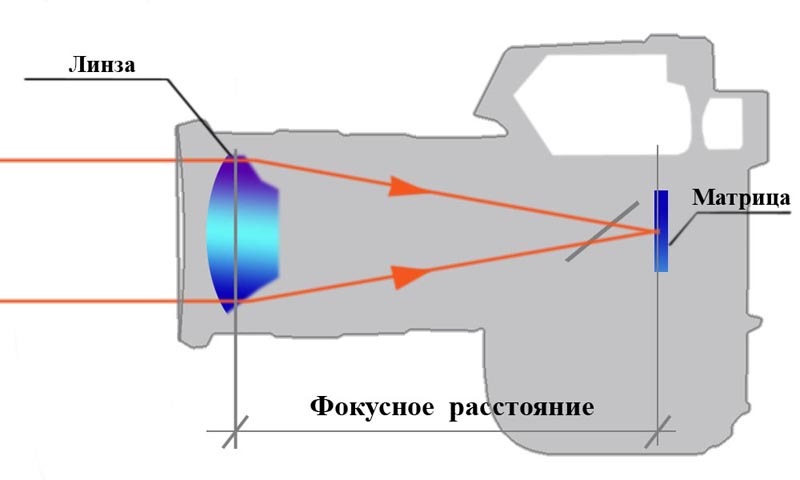
 Сформулировать законы геометрической оптики.
Сформулировать законы геометрической оптики. ..
..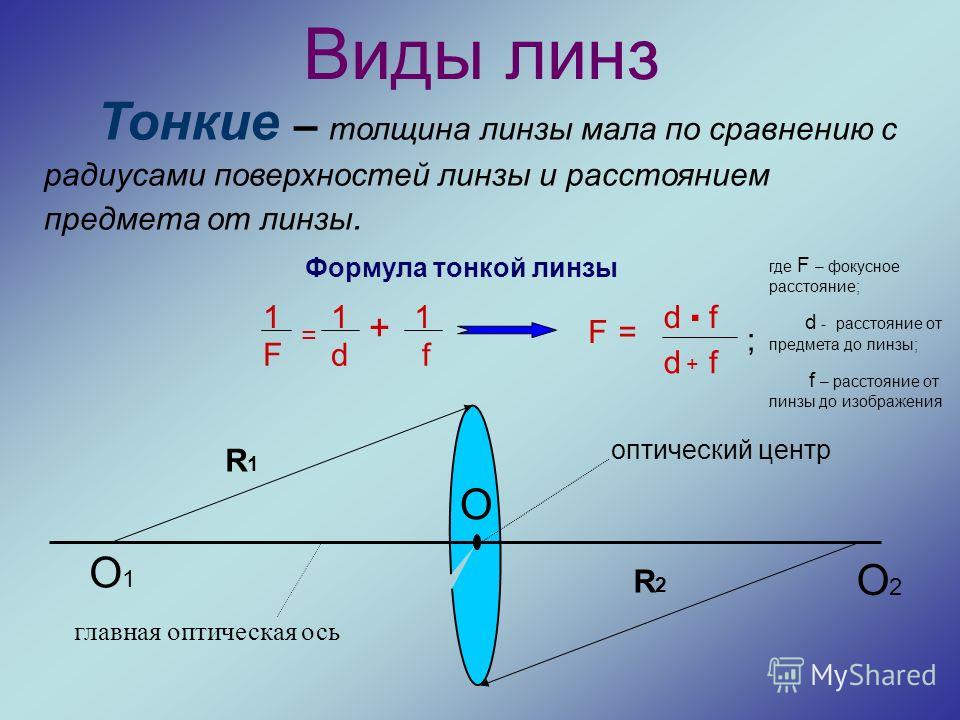 Положение линзы на скамье
(м ).
Положение линзы на скамье
(м ).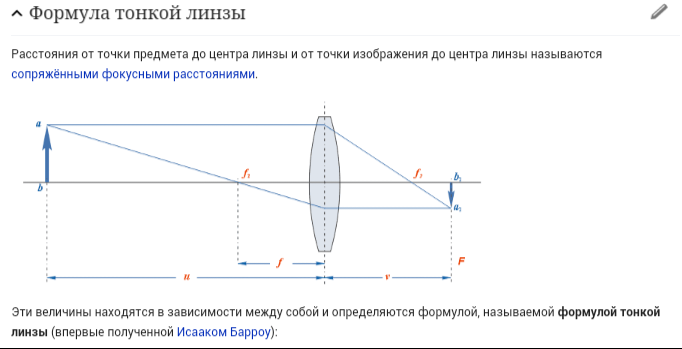 д.
д.
 Для этого необходим дополнительный механический модуль базирования и программный модуль. Это позволяет измерять плoскопараллелность оптических пластин и призм или отклонение от угла 90° y призм. Если у вас возникли сомнения, отвечает ли оборудование вашим потребностям, пожалуйста, свяжитесь с нами. Доступен широкий выбор функций.
Для этого необходим дополнительный механический модуль базирования и программный модуль. Это позволяет измерять плoскопараллелность оптических пластин и призм или отклонение от угла 90° y призм. Если у вас возникли сомнения, отвечает ли оборудование вашим потребностям, пожалуйста, свяжитесь с нами. Доступен широкий выбор функций. Длина волны освещения может быть адаптирована в зависимости от специальных требований. Точность позиционирования измерительной головки (Z — ось)-5 мкм, разрешение-1 мкм. Таким образом, обеспечивается точное определение плоскости положения изображения. Функция автоматической фокусировки позволяет устранить субъективное воздействие оператора на результаты измерений. Во избежание влияния ошибки базирования линзы на результат измерения, используется самоцентрирующийся держатель с диаметром зажима до 100 мм, распространенный в оптической промышленности.
Длина волны освещения может быть адаптирована в зависимости от специальных требований. Точность позиционирования измерительной головки (Z — ось)-5 мкм, разрешение-1 мкм. Таким образом, обеспечивается точное определение плоскости положения изображения. Функция автоматической фокусировки позволяет устранить субъективное воздействие оператора на результаты измерений. Во избежание влияния ошибки базирования линзы на результат измерения, используется самоцентрирующийся держатель с диаметром зажима до 100 мм, распространенный в оптической промышленности.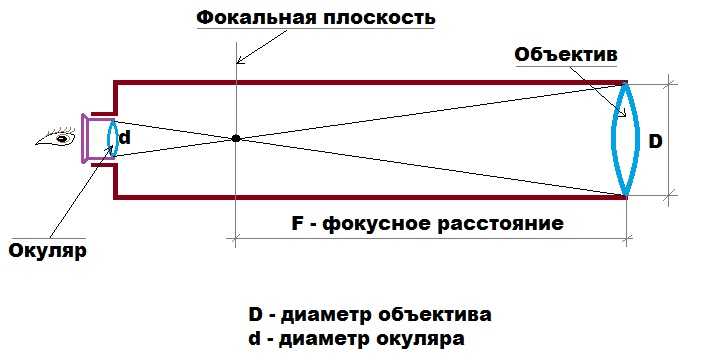 подшипник,
подшипник, Набор базирующих трубок и призм (для различных диаметров линз) поставляется в комплекте с модулем для измерения ошибки базирования. Положения базирующей призмы и фрикционного диска регулируются по трём осям, таким образом они подходят для всех размеров линз. Ошибка центрирования линзы измеряется в проходящем свете при вращении линзы.
Набор базирующих трубок и призм (для различных диаметров линз) поставляется в комплекте с модулем для измерения ошибки базирования. Положения базирующей призмы и фрикционного диска регулируются по трём осям, таким образом они подходят для всех размеров линз. Ошибка центрирования линзы измеряется в проходящем свете при вращении линзы. После контрольного измерения образец помещается под измерительный луч. Измеряется плоскостность.
После контрольного измерения образец помещается под измерительный луч. Измеряется плоскостность.

